家炉と加熱システム §7。確率変数の確率分布密度と数値的特徴

炉と加熱システム

§7。確率変数の確率分布密度と数値的特徴

確率変数 さまざまな状況に応じて特定の値を取ることができる変数であり、 確率変数は連続と呼ばれます 、制限された間隔または無制限の間隔から任意の値を取得できる場合。連続確率変数の場合、すべての可能な値を示すことは不可能であるため、特定の確率に関連付けられたこれらの値の間隔を指定します。

連続確率変数の例には、特定のサイズに研磨される部品の直径、人の身長、発射体の飛行距離などが含まれます。

連続確率変数の場合、関数 F(バツ）、とは異なり 離散確率変数、どこにもジャンプがない場合、連続確率変数の個々の値の確率はゼロです。

これは、連続確率変数の場合、その値間の確率分布について話すのは無意味であることを意味します。つまり、それぞれの値の確率はゼロです。ただし、連続確率変数の値の中には、ある意味「確率の高いものと低いもの」が存在します。たとえば、実際には両方の値が発生する可能性がありますが、確率変数の値（ランダムに遭遇した人の身長 - 170 cm）が 220 cm よりも高い可能性があることを疑う人はほとんどいません。

連続確率変数の分布関数と確率密度

連続確率変数に対してのみ意味をなす分布法則として、分布密度または確率密度の概念が導入されます。連続確率変数と離散確率変数の分布関数の意味を比較して、それにアプローチしてみましょう。

したがって、確率変数の分布関数 (離散と連続の両方)、または 積分関数は、確率変数の値が成立する確率を決定する関数と呼ばれます。バツ制限値以下バツ.

離散確率変数の値の点の場合バツ1 , バツ 2 , ..., バツ私、...大量の確率が集中している p1 , p 2 , ..., p私、...、すべての質量の合計は 1 に等しい。この解釈を連続確率変数の場合に移してみましょう。 1 に等しい質量が個々の点に集中しているのではなく、横軸に沿って連続的に「塗りつけられている」と想像してみましょう。おお多少の濃度ムラがあります。確率変数がいずれかの領域に該当する確率 Δ バツこの領域に属する質量として解釈されます。平均密度このセクションでは - 質量と長さの比として。確率論における重要な概念である分布密度を導入しました。

確率密度 f(バツ) 連続確率変数の分布関数の導関数です。

密度関数を知ると、連続確率変数の値が閉区間に属する確率を見つけることができます。ある; b]:

連続確率変数が存在する確率バツ間隔 [ から任意の値を受け取りますある; b]、以下の範囲の確率密度の特定の積分に等しい。ある前に b:

この場合、関数の一般式は F(バツ) 連続確率変数の確率分布。密度関数がわかっている場合に使用できます。 f(バツ) :

連続確率変数の確率密度グラフは、その分布曲線と呼ばれます (下図)。

曲線、点から引かれた直線で囲まれた図形の領域（図中の網掛け）あるそして b x 軸に垂直、および軸おお、連続確率変数の値が次の確率に達する確率をグラフで表示します。バツの範囲内ですある前に b.

連続確率変数の確率密度関数の性質

1. 確率変数が区間（および関数のグラフによって制限される図形の面積）から任意の値を取る確率 f(バツ) と軸おお) は 1 に等しい:

2. 確率密度関数は負の値を取ることができません。

そして分布の存在外ではその値はゼロです

分布密度 f(バツ)、分布関数と同様に F(バツ) は分布則の形式の 1 つですが、分布関数とは異なり、普遍的ではありません。分布密度は連続確率変数に対してのみ存在します。

実際に連続確率変数の分布の最も重要な 2 つのタイプについて触れてみましょう。

分布密度関数の場合 f(バツ) ある有限区間における連続確率変数 [ ある; b] は定数値をとります C、間隔の外では値が取られますゼロに等しい、それからこれ 分布は均一と呼ばれます .

分布密度関数のグラフが中心に対して対称であれば、平均値は中心付近に集中し、中心から離れるほど平均値から離れたものが集まります（関数のグラフは断面図に似ています）ベル）、それからこれ 分布は正規分布と呼ばれます .

例1.連続確率変数の確率分布関数は次のように知られています。

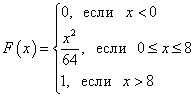
検索機能 f(バツ) 連続確率変数の確率密度。両方の関数のグラフを作成します。連続確率変数が 4 ～ 8 の範囲で任意の値を取る確率を求めます。

解決。確率分布関数の導関数を求めることにより、確率密度関数を取得します。

関数のグラフ F(バツ) - 放物線:

関数のグラフ f(バツ） - 真っ直ぐ：

連続確率変数が 4 ～ 8 の範囲の値を取る確率を求めてみましょう。

例2。連続確率変数の確率密度関数は次のように与えられます。

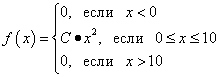
係数の計算 C。検索機能 F(バツ) 連続確率変数の確率分布。両方の関数のグラフを作成します。連続確率変数が 0 ～ 5 の範囲の値を取る確率を求めます。

解決。係数 C確率密度関数のプロパティ 1 を使用して、次のことがわかります。

したがって、連続確率変数の確率密度関数は次のようになります。

積分することで関数がわかります F(バツ) 確率分布。もしバツ < 0 , то F(バツ) = 0 。 0の場合< バツ < 10 , то

バツ> 10 なら F(バツ) = 1 .

したがって、確率分布関数の完全な記録は次のようになります。

関数のグラフ f(バツ) :

関数のグラフ F(バツ) :

連続確率変数が 0 から 5 の範囲の値を取る確率を求めてみましょう。

例 3.連続確率変数の確率密度バツは、とという等式によって与えられます。係数を求めるあ、連続確率変数が存在する確率バツ区間]0、5[、連続確率変数の分布関数から任意の値を受け取りますバツ.

解決。条件によって平等に到達する

したがって、、どこから。それで、

ここで、連続確率変数が存在する確率を求めます。バツ間隔 ]0、5[: の任意の値を受け取ります。

ここで、この確率変数の分布関数を取得します。

例4.連続確率変数の確率密度を求めるバツ、負でない値のみを取ります、およびその分布関数 .

に 離散確率変数の分布関数を見つける、この計算機を使用する必要があります。 演習 1。連続確率変数 X の分布密度は次の形式になります。
探す：
a) パラメータ A;
b) 分布関数 F(x) ;
c) 確率変数 X が区間に入る確率。
G) 期待値 MX と DX の違い。
関数 f(x) と F(x) のグラフを描きます。

タスク 2。積分関数によって与えられる確率変数 X の分散を求めます。

タスク 3。確率変数 X の数学的期待値を求める与えられた関数配布物。

タスク 4。ある確率変数の確率密度は次のように与えられます: f(x) = A/x 4 (x = 1; +∞)
係数 A、分布関数 F(x)、数学的期待値と分散、および確率変数が区間内で値を取る確率を求めます。グラフ f(x) と F(x) を描きます。

タスク。いくつかの連続確率変数の分布関数は次のように与えられます。

パラメーター a と b を決定し、確率密度 f(x)、数学的期待値と分散、および確率変数が区間内で値を取る確率の式を見つけます。 f(x) と F(x) のグラフを描きます。

分布関数の導関数として分布密度関数を求めてみましょう。

知っています

パラメータ a を見つけてみましょう:

または 3a=1、つまり a = 1/3
次のプロパティからパラメーター b を見つけます。
F(4) = a*4 + b = 1
1/3*4 + b = 1 したがって、b = -1/3
したがって、分布関数の形式は次のとおりです: F(x) = (x-1)/3

期待値.

分散.

1 / 9 4 3 - (1 / 9 1 3) - (5 / 2) 2 = 3 / 4
確率変数が区間内で値をとる確率を求めてみましょう
P(2< x< 3) = F(3) – F(2) = (1/3*3 - 1/3) - (1/3*2 - 1/3) = 1/3

例その1。連続確率変数 X の確率分布密度 f(x) が与えられます。必須：

係数Aを決定します。
分布関数 F(x) を求めます。
F(x) と f(x) のグラフを概略的に構築します。
X の数学的な期待値と分散を求めます。
X が区間 (2;3) の値を取る確率を求めます。

f(x) = A*sqrt(x)、1 ≤ x ≤ 4。
解決:

確率変数 X は分布密度 f(x) によって指定されます。

条件からパラメータ A を見つけてみましょう。

または
14/3*A-1 = 0
どこ、
A = 3 / 14

分布関数は次の公式を使用して求めることができます。

4. 連続確率変数の確率密度

連続確率変数は分布関数を使用して指定できます。 F(バツ) 。この割り当て方法は唯一のものではありません。連続確率変数は、分布密度または確率密度と呼ばれる別の関数 (微分関数と呼ばれることもあります) を使用して指定することもできます。

定義4.1: 連続確率変数の分布密度バツ関数を呼び出す f (バツ) - 分布関数の一次導関数 F(バツ) :

f ( バツ ) = F "( バツ ) .

この定義から、分布関数は分布密度の逆微分であることがわかります。分布密度は、離散確率変数の確率分布の説明には適用できないことに注意してください。

連続確率変数が指定された間隔に該当する確率

分布密度がわかれば、連続確率変数が指定された区間に属する値を取る確率を計算できます。

定理： 連続確率変数 X が区間に属する値をとる確率 (ある, b)、と等しい定積分の範囲内で取得した分布密度からある前にb :

証拠：比率を使用します

P(ある ≤ バツb) = F(b) – F(ある).

ニュートン・ライプニッツの公式によれば、

したがって、

なぜなら P(ある ≤ バツ b)= P(あるバツ b) 、そして最終的に得られるのは

幾何学的には、得られた結果は次のように解釈できます。 連続確率変数が区間に属する値を取る確率 (ある, b)、軸で囲まれた曲線台形の面積に等しい牛、分布曲線f(バツ）そしてまっすぐバツ = あるそしてバツ = b.

コメント：特に、 f(バツ) – 関数が偶数で、区間の両端が原点に対して対称である場合、

例。確率変数の確率密度が与えられるバツ

テストの結果、次のような確率が得られる確率を求めます。バツ区間 (0.5, 1) に属する値を取ります。

解決：必要な確率

既知の分布密度から分布関数を求める

分布密度を知る f(バツ) 、分布関数を見つけることができます F(バツ) 式によると

本当に、 F(バツ) = P(バツバツ) = P(-∞ バツ バツ) .

したがって、

したがって、 分布密度がわかれば、分布関数を求めることができます。もちろん、既知の分布関数から分布密度を見つけることができます。、つまり:

f(バツ) = F"(バツ).

例。指定された分布密度の分布関数を求めます。

解決：公式を使ってみましょう

もしバツ ≤ ある、それ f(バツ) = 0 したがって、 F(バツ) = 0 。もし では、 f(x) = 1/(b-a),

したがって、

もしバツ > b、それ

したがって、必要な分布関数は

コメント：一様分布確率変数の分布関数を取得しました (一様分布を参照)。

分布密度の性質

プロパティ 1:分布密度は非負の関数です。

f ( バツ ) ≥ 0 .

プロパティ 2:-∞ から ∞ までの範囲の分布密度の不適切積分は 1 に等しくなります。

コメント：分布密度グラフは次のように呼ばれます。分布曲線.

コメント：連続確率変数の分布密度は分布則とも呼ばれます。

例。確率変数の分布密度は次の形式になります。

定数パラメータを見つけるある.

解決：分布密度は条件を満たす必要があるため、等式が満たされることを要求します。

ここから
。不定積分を求めてみましょう。

不適切な積分を計算してみましょう。

したがって、必要なパラメータは

分布密度の考えられる意味

させて F(バツ) – 連続確率変数の分布関数バツ。分布密度の定義により、 f(バツ) = F"(バツ) 、または

違い F(バツ+Δx) -F(バツ) その確率を決定しますバツ間隔に属する値を取ります (バツ, バツ+Δх)。したがって、連続確率変数が区間に属する値をとる確率比の限界は、 (バツ, バツ+Δх), この間隔の長さまで ( Δx→0) は、点での分布密度の値に等しくなります。バツ.

したがって、関数は f(バツ) 各点の確率分布密度を決定しますバツ。微分積分から、関数の増分は関数の微分にほぼ等しいことが知られています。

なぜなら F"(バツ) = f(バツ) そして DX = ∆ バツ、それ F(バツ+∆ バツ) - F(バツ) ≈ f(バツ)∆ バツ.

この等式の確率的な意味は次のとおりです。 確率変数が区間に属する値を取る確率 (バツ, バツ+∆ バツ) は、点 x における確率密度と区間 Δx の長さの積にほぼ等しい.

幾何学的には、この結果は次のように解釈できます。: 確率変数が区間に属する値を取る確率 (バツ, バツ+∆ バツ) は、底辺 ∆х と高さの長方形の面積にほぼ等しいf(バツ).

5. 離散確率変数の典型的な分布

5.1. ベルヌーイ分布

定義5.1: ランダムな値バツ、2 つの値を取る 1 そして 0 確率（「成功」） pそして（「失敗」） q、と呼ばれるベルヌリエフスカヤ:

, どこ k=0,1.

5.2. 二項分布

生産させてください n 独立したトライアル、それぞれのイベントであ現れるかもしれないし、現れないかもしれない。すべての試行でイベントが発生する確率は一定で等しい p(したがって、非発生確率は q = 1 - p).

確率変数を考えてみるバツ– イベントの発生数あこれらのテストでは。ランダムな値バツ値を受け取ります 0,1,2,… nベルヌーイの公式を使用して計算された確率: 、どこ k = 0,1,2,… n.

定義5.2: 二項はベルヌーイの公式で求められる確率分布と呼ばれます。

例。ターゲットに向かって 3 発のショットが発射され、各ショットが命中する確率は 0.8 です。確率変数を考えてみましょうバツ– ターゲットへのヒット数。その分布シリーズを検索します。

解決：ランダムな値バツ値を受け取ります 0,1,2,3 ベルヌーイの公式を使用して計算された確率で、ここで n = 3, p = 0,8 (命中確率)、 q = 1 - 0,8 = = 0,2 （欠落の可能性）。

したがって、分布系列は次の形式になります。

大きな値にはベルヌーイの公式を使用する nしたがって、対応する確率を計算するには、イベントの発生確率を正確に近似的に求めることができるローカルラプラス定理を使用します。 k 1回に1回 nテストの数が十分に多い場合は、テストを実行します。

局所ラプラス定理: 確率が pイベントの発生あ
その出来事があに登場します n正確にテストする k倍、ほぼ等しい (精度が高いほど、 n) 関数値
, どこ
, .

注1:関数値を含むテーブル
, 付録 1 に記載されており、
. 関数は標準正規分布の密度です (正規分布を参照)。

例：事象が起こる確率を求めてくださいあまさに来るだろう 80 1回に1回 400 各試行でのこのイベントの発生確率が次の試行に等しい場合 0,2.

解決：条件別 n = 400, k = 80, p = 0,2 , q = 0,8 。タスクデータから決まる値を計算してみましょうバツ:
. 付録 1 の表から次のことがわかります。
. この場合、必要な確率は次のようになります。

イベントが発生する確率を計算する必要がある場合は、あに登場します n少なくともテスト k 1 一度だけでもうない k 2 回の場合は、ラプラスの積分定理を使用する必要があります。

ラプラスの積分定理: 確率が pイベントの発生あ各試行の値は一定であり、0 と 1 とは異なります。その場合、確率はその出来事があに登場します nからのテスト k 1 前に k 2 倍、特定の積分にほぼ等しい

, どこ
そして
.

言い換えれば、ある出来事が起こる確率は、あに登場します nからのテスト k 1 前に k 2 倍、ほぼ等しい

どこ
, そして .

注2:関数
これはラプラス関数と呼ばれます (正規分布を参照)。関数値を含むテーブル , 付録 2 に記載されており、
.

例：次の確率を求めてください。 400 部品が品質管理検査に合格しなかった確率が 0,2.

解決：条件別 n = 400, p = 0,2 , q = 0,8, k 1 = 70, k 2 = 100 。積分の下限と上限を計算してみましょう。

;
.

したがって、次のようになります。

付録 2 の表から、次のことがわかります。
そして
. この場合、必要な確率は次のようになります。

注3：一連の独立した試行 (n が大きく、p が小さい場合) では、ポアソン公式を使用して、イベントが正確に k 回発生する確率を計算します (ポアソン分布を参照)。

5.3. ポアソン分布

定義5.3: 離散確率変数は次のように呼ばれます。ポワソン、その分布則が次の形式である場合:

, どこ
そして
(定数値)。

ポアソン確率変数の例:

あたりの通話数自動ステーション一定期間にわたって T.

一定期間にわたるある放射性物質の崩壊粒子の数 T.

一定期間にワークショップに到着したテレビの数 T大都会で .

大都市の交差点の停止線に到着する車の台数 .

注1:これらの確率を計算するための特別な表を付録 3 に示します。

注2:一連の独立したテストで ( n素晴らしい、 pだけでは十分ではありません)、イベントが発生する確率を正確に計算するには kポアソンの公式を使用して次のように計算します。
, どこ
, つまり、イベントの平均発生数は一定のままです。

注3：ポアソンの法則に従って分布する確率変数がある場合、必ず指数則に従って分布する確率変数が存在し、その逆も同様です (指数分布を参照)。

例。基地に送られた植物 5000 良質の製品。製品が輸送中に損傷する確率は次のとおりです。 0,0002 。ちょうど 3 つの使用できない製品が基地に到着する確率を求めます。

解決：条件別 n = 5000, p = 0,0002, k = 3. 見つけます λ: λ = n.p.= 5000·0.0002 = 1.

ポアソンの公式によれば、望ましい確率は次のようになります。

, 確率変数はどこにありますかバツ– 使用できない製品の数。

5.4. 幾何学的分布

独立したテストを実行します。それぞれのテストで、イベントが発生する確率は次のようになります。あに等しい p(0p

q = 1 - p。イベントが表示されるとすぐにチャレンジは終了しますあ。したがって、イベントの場合、あに登場 k- 回目のテスト、その後は前のテスト k – 1 テストでは出ませんでした。

で表しましょうバツ離散確率変数 - イベントが最初に発生するまでに実行する必要がある試行の数あ。明らかに、可能な値はバツは整数 x 1 = 1、x 2 = 2、...

まずしましょう k-1 テストイベントあ来なかったが、入った k-回目のテストが登場しました。この「複雑な事象」の確率は、独立した事象の確率の乗算定理によれば、 P (バツ = k) = q k -1 p.

定義5.4: 離散確率変数には、幾何分布、その分布則が次の形式である場合:

P ( バツ = k ) = q k -1 p , どこ
.

注1:信じる k = 1,2,… 、我々が得る等比数列最初のメンバーと pと分母 q (0q。このため、この分布は幾何学的と呼ばれます。

注2:行
は収束し、その合計は 1 に等しくなります。確かに、級数の合計は次のようになります。
.

例。最初の命中が行われるまで、銃はターゲットに向かって発砲されます。ターゲットに命中する確率 p = 0,6 。 3打目でヒットする確率を求めよ。

解決：条件別 p = 0,6, q = 1 – 0,6 = 0,4, k = 3. 必要な確率は次のとおりです。

P (バツ = 3) = 0,4 2 ·0.6 = 0.096。

5.5. 超幾何分布

次の問題を考えてみましょう。パーティーを外に出しましょう N利用可能な製品 M標準 (MN). バッチからランダムに取得 n(各製品は同じ確率で抽出できます)、選択された製品は次の製品を選択する前にバッチに戻されません (したがって、ベルヌーイの公式はここでは適用できません)。

で表しましょうバツ確率変数 - 数値 メートル中でも定番商品 n選択されました。次に、可能な値はバツ 0、1、2、…、となります。 分; ラベルを付けてみましょう... による独立変数 (Fonds) の値には、ボタン ( 章 ...

この分野の教育および方法論の複合体「一般心理ワークショップ」

トレーニングと測定法の複合体

... 方法論的な 説明書 による実装実務 5.1 几帳面な推奨事項 による教育プロジェクトの実施 5.2 几帳面な推奨事項 による...感度)、 一次元のそして多次元… ランダムのコンポーネント サイズ... と セクション"パフォーマンス...

物理学分野のための教育および方法論の複合体 (タイトル)

トレーニングと測定法の複合体

... セクション教科書では。問題解決 によるそれぞれのトピック。詳細 方法論的な 説明書研究室での作業用 による ... ランダムおよび機器測定誤差 1.8 トピックステストそして 方法論的な 説明書 による... 粒子が入っている 一次元の潜在的な穴。 ...

コンピューターサイエンス分野における実験作業のガイドライン

ガイドライン

... 几帳面な 説明書に研究室での作業 による ... サイズ、そして最大の金額量... 配列 ランダム数値... 3.0 4.0 3.0 -2.5 14.3 16.2 18.0 1.0 a) 一次元の配列 b) 2 次元配列図 2 – ファイルについては...で説明されています。 セクション実装後の...

確率変数変数は、各テストの結果として、ランダムな理由に応じて、以前は未知の 1 つの値を取る変数と呼ばれます。ランダム変数ラテン語の大文字で示されます: $X,\ Y,\ Z,\ \dots $ 確率変数はその種類によって次のようになります。離散そして 継続的な.

離散確率変数- これは、値が可算以下、つまり有限または可算のいずれかである確率変数です。可算性とは、確率変数の値に番号を付けることができることを意味します。

例1 。離散確率変数の例を次に示します。

a) $n$ ショットによるターゲットへのヒット数。ここで可能な値は、$0、\ 1、\ \dots、\ n$ です。

b) コインを投げたときにドロップされるエンブレムの数。ここで可能な値は、$0、\ 1、\ \dots、\ n$ です。

c) 到着する船の数 (可算値のセット)。

d) PBX に到着するコールの数 (可算値のセット)。

1. 離散確率変数の確率分布の法則。

離散確率変数 $X$ は、確率 $p\left(x_1\right),\ \dots ,\ p\left(x_n\right)$ を持つ値 $x_1,\dots ,\ x_n$ を取ることができます。これらの値とその確率の間の対応はと呼ばれます 離散確率変数の分布の法則。原則として、この対応関係はテーブルを使用して指定されます。テーブルの最初の行には $x_1,\dots ,\ x_n$ の値が示され、2 行目にはそれに対応する確率 $p_1,\dots ,\ p_n$ が含まれています。これらの値。

$\begin(配列)(|c|c|)
\hline
X_i & x_1 & x_2 & \ドット & x_n \\
\hline
p_i & p_1 & p_2 & \ドット & p_n \\
\hline
\end(配列)$

例 2 。確率変数 $X$ をサイコロを投げたときに出る点の数とします。このような確率変数 $X$ は、$1、\ 2、\ 3、\ 4、\ 5、\ 6$ の値を取ることができます。これらすべての値の確率は $1/6$ に等しくなります。次に、確率変数 $X$ の確率分布の法則は次のようになります。

$\begin(配列)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline

\hline
\end(配列)$

コメント。離散確率変数 $X$ の分布法則では、イベント $1,\ 2,\ \dots ,\ 6$ がイベントの完全なグループを形成するため、確率の合計は 1、つまり $ に等しくなければなりません。 \sum(p_i)=1$。

2. 離散確率変数の数学的期待。

確率変数の期待値その「中心」の意味を設定します。離散確率変数の場合、数学的期待値は、値 $x_1,\dots ,\ x_n$ とこれらの値に対応する確率 $p_1,\dots ,\ p_n$ の積の合計として計算されます。 : $M\left(X\right)=\sum ^n_(i=1)(p_ix_i)$。英語文献では、別の表記 $E\left(X\right)$ が使用されます。

数学的期待値の性質$M\左(X\右)$:

$M\left(X\right)$ は最小値と最小値の間に含まれます。最高値確率変数 $X$。
定数の数学的期待は定数自体と等しい、つまり $M\left(C\right)=C$。
定数因数は、数学的期待値の符号から取り出すことができます: $M\left(CX\right)=CM\left(X\right)$。
確率変数の合計の数学的期待値は、それらの数学的期待値の合計に等しくなります: $M\left(X+Y\right)=M\left(X\right)+M\left(Y\right)$。
独立確率変数の積の数学的期待値は、数学的期待値の積に等しい: $M\left(XY\right)=M\left(X\right)M\left(Y\right)$。

例 3 。例 $2$ から確率変数 $X$ の数学的期待値を求めてみましょう。

$$M\left(X\right)=\sum^n_(i=1)(p_ix_i)=1\cdot ((1)\over (6))+2\cdot ((1)\over (6) )+3\cdot ((1)\over (6))+4\cdot ((1)\over (6))+5\cdot ((1)\over (6))+6\cdot ((1) )\over (6))=3.5.$$

$M\left(X\right)$ は、確率変数 $X$ の最小値 ($1$) と最大値 ($6$) の間にあることがわかります。

例 4 。確率変数 $X$ の数学的期待値は $M\left(X\right)=2$ に等しいことが知られています。確率変数 $3X+5$ の数学的期待値を求めます。

上記のプロパティを使用すると、 $M\left(3X+5\right)=M\left(3X\right)+M\left(5\right)=3M\left(X\right)+5=3\ が得られます。 cdot 2 +5=11$。

例5 。確率変数 $X$ の数学的期待値は $M\left(X\right)=4$ に等しいことが知られています。確率変数 $2X-9$ の数学的期待値を求めます。

上記のプロパティを使用すると、 $M\left(2X-9\right)=M\left(2X\right)-M\left(9\right)=2M\left(X\right)-9=2\ が得られます。 cdot 4 -9=-1$。

3. 離散確率変数の分散。

数学的期待値が等しい確率変数の可能な値は、平均値の周囲で異なる分散を示す可能性があります。たとえば、2 つの学生グループで GPA確率論の試験では結果は 4 でしたが、一方のグループでは全員が優秀な生徒であることが判明し、もう一方のグループでは C の生徒と優秀な生徒だけが集まりました。したがって、数学的期待を中心とした確率変数の値の広がりを示す、確率変数の数値特性が必要です。この特性が分散です。

離散確率変数の分散$X$ は次と同じです:

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2).\ $$

英語文献では、$V\left(X\right),\ Var\left(X\right)$ という表記が使用されます。多くの場合、分散 $D\left(X\right)$ は、式 $D\left(X\right)=\sum^n_(i=1)(p_ix^2_i)-(\left(M\) を使用して計算されます。 left(X \right)\right))^2$。

分散特性$D\左(X\右)$:

分散は常にゼロ以上です。つまり、 $D\left(X\right)\ge 0$。
定数の分散はゼロです。 $D\左(C\右)=0$。
定数係数は、分散の符号が 2 乗である場合、分散の符号から取り出すことができます。 $D\left(CX\right)=C^2D\left(X\right)$。
独立した確率変数の合計の分散は、それらの分散の合計に等しくなります。 $D\left(X+Y\right)=D\left(X\right)+D\left(Y\right)$。
独立した確率変数間の差の分散は、それらの分散の合計に等しくなります。 $D\left(X-Y\right)=D\left(X\right)+D\left(Y\right)$。

例6 。例 $2$ から確率変数 $X$ の分散を計算してみましょう。

$$D\left(X\right)=\sum^n_(i=1)(p_i(\left(x_i-M\left(X\right)\right))^2)=((1)\over (6))\cdot (\left(1-3.5\right))^2+((1)\over (6))\cdot (\left(2-3.5\right))^2+ \dots +( (1)\over (6))\cdot (\left(6-3.5\right))^2=((35)\over (12))\約 2.92.$$

例 7 。確率変数 $X$ の分散は $D\left(X\right)=2$ に等しいことが知られています。確率変数 $4X+1$ の分散を求めます。

上記のプロパティを使用すると、 $D\left(4X+1\right)=D\left(4X\right)+D\left(1\right)=4^2D\left(X\right)+0= がわかります。 16D\左(X\右)=16\cdot 2=32$。

例8 。確率変数 $X$ の分散は $D\left(X\right)=3$ に等しいことが知られています。確率変数 $3-2X$ の分散を求めます。

上記のプロパティを使用すると、 $D\left(3-2X\right)=D\left(3\right)+D\left(2X\right)=0+2^2D\left(X\right)= がわかります。 4D\左(X\右)=4\cdot 3=12$。

4. 離散確率変数の分布関数。

離散確率変数を分布系列の形で表現する方法は唯一の方法ではありません。そして最も重要なことに、連続確率変数は分布系列を使用して指定できないため、この方法は普遍的ではありません。確率変数を表す別の方法として、分布関数があります。

分布関数確率変数 $X$ は関数 $F\left(x\right)$ と呼ばれ、確率変数 $X$ が固定値 $x$ より小さい値を取る確率、つまり $F\ を決定します。 left(x\right )=P\left(X< x\right)$

分布関数の性質:

$0\le F\left(x\right)\le 1$。
確率変数 $X$ が区間 $\left(\alpha ;\ \beta \right)$ の値を取る確率は、この両端の分布関数の値の差に等しい間隔: $P\left(\alpha< X < \beta \right)=F\left(\beta \right)-F\left(\alpha \right)$
$F\left(x\right)$ - 減少しません。
$(\mathop(lim)_(x\to -\infty ) F\left(x\right)=0\ ),\ (\mathop(lim)_(x\to +\infty ) F\left(x \right)=1\ )$。

例9 。例 $2$ からの離散確率変数 $X$ の分布法則に対する分布関数 $F\left(x\right)$ を見つけてみましょう。

$\begin(配列)(|c|c|)
\hline
1 & 2 & 3 & 4 & 5 & 6 \\
\hline
1/6 & 1/6 & 1/6 & 1/6 & 1/6 & 1/6 \\
\hline
\end(配列)$

$x\le 1$ の場合、明らかに $F\left(x\right)=0$ ($x=1$ の場合も $F\left(1\right)=P\left(X< 1\right)=0$).

1ドルの場合< x\le 2$, то $F\left(x\right)=P\left(X=1\right)=1/6$.

2ドルの場合< x\le 3$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)=1/6+1/6=1/3$.

3ドルなら< x\le 4$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)=1/6+1/6+1/6=1/2$.

4ドルなら< x\le 5$, то $F\left(X\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)=1/6+1/6+1/6+1/6=2/3$.

5ドルなら< x\le 6$, то $F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right)+P\left(X=4\right)+P\left(X=5\right)=1/6+1/6+1/6+1/6+1/6=5/6$.

$x > 6$ の場合、$F\left(x\right)=P\left(X=1\right)+P\left(X=2\right)+P\left(X=3\right) +P\左(X=4\右)+P\左(X=5\右)+P\左(X=6\右)=1/6+1/6+1/6+1/6+ 1/6+1/6=1$。

つまり $F(x)=\left\(\begin(行列)
0,\ at\ x\le 1,\\
1/6、\1で< x\le 2,\\
1/3、\ 2< x\le 3,\\
1/2、\3で< x\le 4,\\
2/3、\ 4< x\le 5,\\
5/6、\4で< x\le 5,\\
1,\ for\ x > 6.
\end(行列)\right.$

連続確率変数 (微分分布関数) の確率分布密度は、積分分布関数の 1 次導関数です: f(x)=F’(X)。この定義と分布関数の特性から、次のことがわかります。

連続確率変数 X の数学的期待値は次の数値です。

連続確率変数 X の分散は次の式によって決定されます。

例79。時間分布密度 T生産ラインでの REA 組み立て

係数を求めるあ、REA 組み立て時間の分布関数、および組み立て時間が間隔 (0.1A) 内に収まる確率。

解決。確率変数の分布関数の性質に基づく

部分ごとに 2 回積分すると、次のようになります。

分布関数は次と等しい

REA の組み立て時間が制限を超えない確率 (0; 1/λ):

例80。電子機器本体の出力抵抗の公称値からの偏差の確率密度 R 0 公差範囲内では 2δ は法則で記述されます

公称値からの抵抗偏差の数学的期待値と分散を求めます。

解決。

被積分関数が奇数であり、積分の極限が原点に関して対称であるため、積分は 0 に等しくなります。

したがって、 M{R} = 0.

置き換えを行うことで r = ある罪バツ, 我々が得る

例81。連続確率変数 X の分布密度は次のように与えられます。

検索: 1. F(x); 2.M(X); 3.D(X)。

解決。 1. F(x) を求めるには、次の式を使用します。

もし
、それ

あ

もし
、それ

もし
、f(x)=0、そして

部分ごとに 2 回積分すると、次のようになります。

、それから

82. 問題 74、75 で f(x)、M(X)、D(X) を求めます。

83. 連続確率変数 X の分布密度は次のように与えられます。

分布関数 F(x) を求めます。

84. 連続確率変数 X の分布密度は、Ox 軸全体で次の式で与えられます。
。定数パラメーター C を見つけます。

85. 区間 (-3, 3) の確率変数 X は分布密度によって与えられます。
; この間隔の外では

a) X の分散を求めます。

b) どちらの可能性が高いか: テストの結果は X になります<1 или X>1?

86. 分布関数によって与えられる確率変数 X の分散を求めます

87. 確率変数は分布関数で与えられる

期待値、分散、平均を求める標準偏差バツ。

§8. 一様分布と指数分布

連続確率変数 X の分布は、X のすべての可能な値を含む区間 (a,b) 上で密度が一定のままであり、この区間の外側ではゼロである場合、均一であると呼ばれます。

指数分布は連続確率変数 X の確率分布であり、密度によって記述されます。

ここで、λ は正の定数値です。指数則分布関数

数学的な期待値と分散はそれぞれ等しい

;
;

例88。電流計の目盛値は0.10Aです。電流計の測定値は、最も近い整数の桁に四捨五入されます。カウント中に 0.02A を超える誤差が発生する確率を求めます。

解決。丸め誤差は、2 つの整数除算の間の間隔 (0;0.1) に均一に分布する確率変数 X として考えることができます。したがって、

それから
.

例89。要素が故障せずに動作する期間は指数関数的に分布します。 t=100 時間の期間中に次の確率を求めます。 a) 要素が故障する。 b) 要素は故障しません。

解決。 a) 定義上
したがって、時間 t における要素の故障の確率が決まります。

b) 「要素は故障しない」という事象は考慮されている事象とは逆であるため、その確率は

90. 無線電子ユニットは生産ラインで組み立てられ、組み立てサイクルは 2 分です。完成したブロックは、クロックサイクル内の任意の時点で監視および調整のためにコンベアから取り出されます。完成したブロックがコンベア上にある時間の数学的期待値と標準偏差を求めます。ブロックがコンベア上で費やす時間は、確率変数の一様分布の法則に従います。

91. 一定時間内に REA が失敗する確率は次の式で表されます。。電子機器が故障するまでの平均稼働時間を決定します。

92. 開発中の通信衛星は、平均故障間隔が 5 年でなければなりません。故障間のリアルタイム時間をランダムな指数分布値とみなして、次の確率を決定します。

a) 衛星の運用期間は 5 年未満です。

b) 衛星は少なくとも 10 年間運用されます。

c) 衛星は 6 年以内に故障する。

93. ある入居者は、平均寿命が 1000 時間の白熱電球を 4 つ購入し、そのうちの 1 つを電気スタンドに取り付け、残りはランプが切れた場合に備えて保管していました。定義する：

a) 4 つのランプの予想される合計耐用年数、

b) 4 つのランプが合計 5000 時間以上動作する確率、

c) すべてのランプの総耐用年数が 2000 時間を超えない確率。

94. スケール分割価格測定器 0.2に等しい。機器の測定値は、最も近い整数の単位に四捨五入されます。計数中にエラーが発生する確率を求めます。 a) 0.04 未満。 b) 大きい 0.05。

95. 特定の路線のバスは、厳密に時刻表通りに運行します。移動間隔5分停留所に到着した乗客が次のバスまでの待ち時間が 3 分未満である確率を求めます。

96. 区間 (2, 8) に均一に分布する確率変数 X の数学的期待値を求めます。

97. 区間 (2, 8) 内に均一に分布する確率変数 X の分散と標準偏差を求めます。

98. 2 つの独立して動作する要素がテストされます。最初の要素の障害のない動作の継続時間は指数関数的に分布します。
、 2番
。 t=6 時間の期間中に次の確率を求めます。 a) 両方の要素が故障する。 b) 両方の要素が失敗することはありません。 c) 1 つの要素のみが失敗します。 d) 少なくとも 1 つの要素が失敗します。