等次一次方程式系

均質なシステム 一次方程式形式のシステムと呼ばれる

この場合は明らかです 、 なぜなら これらの行列式のいずれかの列のすべての要素はゼロに等しくなります。

未知数は公式に従って求められるので、 、Δ ≠ 0 の場合、システムは固有のゼロ解を持ちます。 バツ = y = z= 0。ただし、多くの問題で興味深い問題は、均質系にゼロ以外の解があるかどうかです。

定理。リニアシステムのために 同次方程式の解がゼロでない場合、Δ ≠ 0 であることが必要かつ十分です。

したがって、行列式 Δ ≠ 0 の場合、システムには固有の解が存在します。 Δ ≠ 0 の場合、線形同次方程式系には無限の数の解があります。

例。

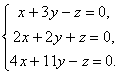
行列の固有ベクトルと固有値

正方行列が与えられるとします , バツ– いくつかの行列列。その高さは行列の次数と一致します。 あ. .

多くの問題では、次の方程式を考慮する必要があります。 バツ

ここで、λ は特定の数です。 任意の λ に対して、この方程式にはゼロ解があることは明らかです。

この方程式がゼロ以外の解を持つ数 λ は と呼ばれます。 固有値行列 あ、A バツこのような λ は次のように呼ばれます 固有ベクトル行列 あ.

行列の固有ベクトルを求めてみましょう あ。 なぜなら E∙X = Xの場合、行列方程式は次のように書き換えることができます。 または 。 拡張形式では、この方程式は連立一次方程式として書き直すことができます。 本当に .

したがって

したがって、座標を決定するための同次一次方程式系が得られました。 ×1, ×2, ×3ベクター バツ。 システムが非ゼロの解を持つためには、システムの行列式がゼロに等しいことが必要かつ十分です。

これは λ の 3 次方程式です。 それは呼ばれています 特性方程式行列 あλ の固有値を決定するのに役立ちます。

各固有値 λ は固有ベクトルに対応します バツ、その座標は対応する λ の値でシステムから決定されます。

例。

ベクトル代数。 ベクトルの概念

物理学のさまざまな分野を研究する場合、長さ、面積、質量、温度など、数値を指定することによって完全に決定される量があります。 このような量はスカラーと呼ばれます。 ただし、それらに加えて、物体に作用する力、物体の速度や加速度など、数値に加えて空間内の方向を知る必要がある量もあります。空間を移動するときの体、張力 磁場空間内の特定の点などで このような量はベクトル量と呼ばれます。

厳密な定義を紹介しましょう。

有向セグメントどちらが最初でどちらが 2 番目であるかがわかっている端を基準にして、セグメントを呼び出しましょう。

ベクター特定の長さを持つ有向セグメントと呼ばれます。 これは特定の長さのセグメントであり、それを制限する点の 1 つが開始点とみなされ、2 番目の点が終了点と見なされます。 もし あ– ベクトルの先頭、 Bが終端である場合、ベクトルは記号で示され、さらにベクトルは 1 つの文字で示されることがよくあります。 図では、ベクトルは線分で示され、その方向は矢印で示されています。

モジュールまたは 長さベクトルは、それを定義する有向セグメントの長さと呼ばれます。 || で示される または || 。

始まりと終わりが一致する、いわゆるゼロ ベクトルもベクトルとして含めます。 指定されております。 ゼロ ベクトルには特定の方向はなく、その係数は ゼロに等しい ||=0.

ベクトルは次のように呼ばれます 同一直線上にある、それらが同じ線上または平行線上にある場合。 また、ベクトル と が同じ方向の場合は、 、反対 と書きます。

同じ平面に平行な直線上にあるベクトルを と呼びます。 同一平面上にある.

2 つのベクトルは次のように呼ばれます。 等しい、同一線上にある場合は、方向が同じで長さが等しいことを意味します。 この場合、彼らは と書きます。

ベクトルの等価性の定義から、ベクトルは空間内の任意の点に原点を置き、それ自体と平行に輸送できることがわかります。

例えば.

ベクトルの線形演算

1. ベクトルと数値の乗算。

   ベクトルと数値 λ の積は、次のような新しいベクトルです。

   ベクトルと数値 λ の積は で表されます。

   

   例えば、ベクトルと同じ方向を向き、ベクトルの半分の長さを持つベクトルが存在します。

   導入された操作は次のとおりです プロパティ:

2. ベクトルの追加。

   と を 2 つの任意のベクトルとしましょう。 任意の点を取ってみましょう ○そしてベクトルを構築します。 その後は要点から あベクトルは脇に置いておきましょう。 最初のベクトルの始まりと 2 番目のベクトルの終わりを接続するベクトルは、 額これらのベクトルの で表されます。 .

   

   ベクトル加算の定式化された定義は次のように呼ばれます。 平行四辺形の法則, 同じベクトルの合計が次のように得られるためです。 その点から先延ばしにしましょう ○ベクトルと . これらのベクトルで平行四辺形を作図しましょう OABC。 ベクトルなので、頂点から描かれた平行四辺形の対角線であるベクトルになります。 ○、明らかにベクトルの合計になります。

   

   以下のことを簡単に確認できます ベクトル加算の性質.

3. ベクトルの違い。

   与えられたベクトルと同一直線上にあり、長さが等しく、反対方向を向いているベクトルをと呼びます。 反対ベクトルの場合はベクトルであり、 で表されます。 逆のベクトルは、ベクトルに数値 λ = –1 を乗算した結果と考えることができます。

対角行列は最も単純な構造を持っています。 線形演算子の行列が対角形式になる基底を見つけることができるかどうかという疑問が生じます。 そのような根拠が存在します。
線形空間 R n とその中で作用する線形演算子 A が与えられるとします。 この場合、演算子 A は R n をそれ自体に取り込みます。つまり、 A:R n → R n です。

意味。 演算子 A が共線ベクトルに変換される場合、非ゼロ ベクトルは演算子 A の固有ベクトルと呼ばれます。 数値 λ は固有値または演算子 A の固有値と呼ばれ、固有ベクトルに対応します。
固有値と固有ベクトルのいくつかの性質に注目してみましょう。
1. 固有ベクトルの任意の線形結合 同じ固有値 λ に対応する演算子 A は、同じ固有値を持つ固有ベクトルです。
2. 固有ベクトル ペアごとに異なる固有値 λ 1 、 λ 2 、…、 λ m を持つ演算子 A は線形独立です。
3. 固有値 λ 1 =λ 2 = λ m = λ の場合、固有値 λ は m 個の線形独立固有ベクトルに対応します。

したがって、線形に独立した固有ベクトルが n 個ある場合、 、異なる固有値 λ 1 、 λ 2 、...、 λ n に対応する場合、それらは線形独立であるため、空間 R n の基礎として取ることができます。 固有ベクトルに基づいて線形演算子 A の行列の形式を見つけてみましょう。これについては、基底ベクトルに基づいて演算子 A を操作します。 それから .
したがって、固有ベクトルに基づく線形演算子 A の行列は対角形式を持ち、演算子 A の固有値は対角に沿っています。
行列が対角形になる別の根拠はありますか? この質問に対する答えは、次の定理によって得られます。

定理。 基底 (i = 1..n) 内の線形演算子 A の行列は、基底のすべてのベクトルが演算子 A の固有ベクトルである場合に限り、対角形式になります。

固有値と固有ベクトルを求めるためのルール

ベクトルを与えてみましょう ここで、x 1、x 2、…、x n は基底を基準としたベクトルの座標です。 は、固有値 λ に対応する線形演算子 A の固有ベクトルです。 この関係は行列形式で書くことができます

. (*)

方程式 (*) は、 と を見つけるための方程式と考えることができます。つまり、次のことに興味があります。 重要な解決策、固有ベクトルをゼロにすることはできないためです。 同次一次方程式系の非自明な解は、det(A - λE) = 0 の場合にのみ存在することが知られています。したがって、λ が演算子 A の固有値であるためには、det(A - λE) であることが必要かつ十分です。 ) = 0。
方程式 (*) を座標形式で詳細に記述すると、次の線形均質方程式系が得られます。

(1)
どこ - 線形演算子行列。

システム (1) の行列式 D がゼロに等しい場合、システム (1) は非ゼロの解になります。

固有値を求める方程式を受け取りました。
この方程式は特性方程式と呼ばれ、その左側は行列 (演算子) A の特性多項式と呼ばれます。特性多項式に実根がない場合、行列 A は固有ベクトルを持たず、対角形式に還元できません。
λ 1 、 λ 2 、…、 λ n を特性方程式の実根とし、それらの間には倍数が存在する可能性があります。 これらの値を系 (1) に順番に代入すると、固有ベクトルが見つかります。

例12。 線形演算子 A は、法則に従って R 3 で作用します。ここで、x 1、x 2、...、x n は基底内のベクトルの座標です。 , , 。 この演算子の固有値と固有ベクトルを求めます。
解決。 この演算子の行列を構築します。
.
固有ベクトルの座標を決定するシステムを作成します。

コンパイル中 特性方程式そしてそれを解決します:

.
λ 1,2 = -1、λ 3 = 3。
系に λ = -1 を代入すると、次のようになります。
または
なぜなら の場合、2 つの従属変数と 1 つの自由変数が存在します。
x 1 を自由な未知数とすると、 この系を何らかの方法で解いて見つけます。 共通の決定この系の: n - r = 3 - 2 = 1 であるため、基本的な解系は 1 つの解で構成されます。
固有値 λ = -1 に対応する固有ベクトルのセットは次の形式になります。ここで、x 1 はゼロ以外の任意の数です。 このセットからベクトルを 1 つ選択してみましょう。たとえば、x 1 = 1 とします。 .
同様の推論で、固有値 λ = 3 に対応する固有ベクトルが見つかります。 .
空間 R 3 では、基底は 3 つの線形独立ベクトルで構成されますが、受け取ったのは 2 つの線形独立固有ベクトルのみであり、そこから R 3 の基底を構成することはできません。 したがって、線形演算子の行列 A を対角形式に還元することはできません。

例13。 行列が与えられると .
1. ベクトルが は行列 A の固有ベクトルです。この固有ベクトルに対応する固有値を見つけます。
2. 行列 A が対角形式を持つ基底を見つけます。
解決。
1. の場合、 は固有ベクトルです

.
ベクトル (1, 8, -1) は固有ベクトルです。 固有値 λ = -1。
行列は固有ベクトルからなる基底で対角形式をとります。 そのうちの1つは有名です。 残りを探してみましょう。
システムから固有ベクトルを探します。

特性方程式: ;
(3 + λ)[-2(2-λ)(2+λ)+3] = 0; (3+λ)(λ 2 - 1) = 0
λ 1 = -3、λ 2 = 1、λ 3 = -1。
固有値 λ = -3 に対応する固有ベクトルを見つけてみましょう。

このシステムの行列のランクは 2 であり、 数値に等しい未知数であるため、このシステムにはゼロ解 x 1 = x 3 = 0 しかありません。ここでの x 2 はゼロ以外の値、たとえば x 2 = 1 にすることができます。したがって、ベクトル (0,1,0) は固有ベクトルです。 、 λ = -3 に対応します。 確認しよう：
.
λ = 1 の場合、次のシステムが得られます。
マトリックスのランクは 2 です。 最後の式を取り消し線で消します。
x 3 を自由な未知数とします。 したがって、x 1 = -3x 3、4x 2 = 10x 1 - 6x 3 = -30x 3 - 6x 3、x 2 = -9x 3 となります。
x 3 = 1 と仮定すると、固有値 λ = 1 に対応する固有ベクトル (-3,-9,1) が得られます。以下を確認してください。

.
固有値は実数で個別であるため、それらに対応するベクトルは線形独立であるため、R 3 の基礎として使用できます。 したがって、基本的には , , 行列 A の形式は次のとおりです。
.
一部の線形演算子では線形独立固有ベクトルが n 個未満である可能性があるため、線形演算子のすべての行列 A:R n → R n を対角形式に縮小できるわけではありません。 ただし、行列が対称の場合、多重度 m の特性方程式の根は、正確に m 個の線形独立ベクトルに対応します。

意味。 対称行列は、主対角に関して対称な要素が等しい正方行列です。つまり、 です。
ノート。 1. 対称行列の固有値はすべて実数です。
2. ペアごとに異なる固有値に対応する対称行列の固有ベクトルは直交します。
研究した装置の多くの応用例の 1 つとして、2 次曲線のタイプを決定する問題を検討します。

正方行列の固有ベクトルは、特定の行列を乗算すると共線ベクトルが得られるものです。 簡単な言葉で言うと、行列に固有ベクトルを乗算すると、後者は同じままですが、特定の数が乗算されます。

意味

固有ベクトルは非ゼロベクトル V であり、正方行列 M を乗算すると、それ自体が何らかの数 λ だけ増加します。 で 代数表記それは次のようになります:

M × V = λ × V、

ここで、 λ は行列 M の固有値です。

考えてみましょう 数値例。 記録を容易にするために、行列内の数値はセミコロンで区切られます。 マトリックスを考えてみましょう:

• M = 0; 4;
• 6; 10.

これに列ベクトルを乗算してみましょう。

• V = -2;

行列に列ベクトルを乗算すると、列ベクトルも得られます。 厳しい 数学的言語 2 × 2 行列と列ベクトルを乗算する式は次のようになります。

• M × V = M11 × V11 + M12 × V21;
• M21×V11＋M22×V21。

Ｍ１１は行列Ｍの１行１列に位置する要素を意味し、Ｍ２２は２行２列に位置する要素を意味する。 私たちの行列の場合、これらの要素は M11 = 0、M12 = 4、M21 = 6、M22 10 に等しくなります。列ベクトルの場合、これらの値は V11 = –2、V21 = 1 に等しくなります。この式によれば、我々が得る 次の結果正方行列とベクトルの積：

• M × V = 0 × (-2) + (4) × (1) = 4;
• 6 × (-2) + 10 × (1) = -2。

便宜上、列ベクトルを行に書き込みましょう。 そこで、正方行列にベクトル (-2; 1) を乗算し、ベクトル (4; -2) を求めました。 明らかに、これは同じベクトルに λ = -2 を掛けたものです。 この場合のラムダは行列の固有値を示します。

行列の固有ベクトルは共線ベクトル、つまり行列を乗算しても空間内の位置が変わらないオブジェクトです。 ベクトル代数における共線性の概念は、幾何学の並列性という用語に似ています。 幾何学的な解釈では、共線ベクトルは、異なる長さの平行な有向セグメントです。 ユークリッドの時代から、1 つの直線にはそれに平行な無限の数の直線があることがわかっているため、各行列が無限の数の固有ベクトルを持つと仮定するのは論理的です。

前の例から、固有ベクトルが (-8; 4)、(16; -8)、および (32, -16) になる可能性があることは明らかです。 これらはすべて、固有値 λ = -2 に対応する共線ベクトルです。 元の行列にこれらのベクトルを乗算しても、元の行列とは 2 倍異なるベクトルが得られます。 そのため、固有ベクトルを求める問題を解く際には、線形に独立したベクトル オブジェクトのみを見つける必要があります。 ほとんどの場合、n × n 行列の場合、n 個の固有ベクトルが存在します。 私たちの計算機は 2 次正方行列の解析用に設計されているため、一致する場合を除いて、ほとんどの場合、結果では 2 つの固有ベクトルが見つかります。

上の例では、元の行列の固有ベクトルが事前にわかっており、ラムダ数が明確に決定されました。 ただし、実際には、すべてが逆に起こります。最初に固有値が見つかり、次に固有ベクトルが見つかります。

解法アルゴリズム

元の行列 M をもう一度見て、その両方の固有ベクトルを見つけてみましょう。 したがって、行列は次のようになります。

• M = 0; 4;
• 6; 10.

まず固有値 λ を決定する必要があります。これには次の行列の行列式を計算する必要があります。

• (0 − λ); 4;
• 6; (10 − λ)。

この行列は、主対角上の要素から未知の λ を減算することによって取得されます。 行列式は、次の標準式を使用して決定されます。

• detA = M11 × M21 − M12 × M22
• detA = (0 − λ) × (10 − λ) − 24

ベクトルはゼロ以外でなければならないため、結果として得られる方程式を線形従属として受け入れ、行列式 detA をゼロとみなします。

(0 − λ) × (10 − λ) − 24 = 0

括弧を開いて行列の特性方程式を取得しましょう。

λ 2 − 10λ − 24 = 0

これは標準です 二次方程式、これは判別式によって解決する必要があります。

D = b 2 − 4ac = (-10) × 2 − 4 × (-1) × 24 = 100 + 96 = 196

判別式の根は sqrt(D) = 14 であるため、λ1 = -2、λ2 = 12 となります。ここで、各ラムダ値について固有ベクトルを見つける必要があります。 λ = -2 のシステム係数を表してみましょう。

• M − λ × E = 2; 4;
• 6; 12.

この式では、E は単位行列です。 結果の行列に基づいて、線形方程式系を作成します。

2x + 4y = 6x + 12y、

ここで、x と y は固有ベクトル要素です。

左側のすべての X と右側のすべての Y を集めましょう。 明らかに、4x = 8y です。 式を - 4 で割ると、x = –2y が得られます。 これで、未知数の任意の値を取得して、行列の最初の固有ベクトルを決定できます (線形に依存する固有ベクトルが無限大であることを思い出してください)。 y = 1、x = –2 とします。 したがって、最初の固有ベクトルは V1 = (–2; 1) のようになります。 記事の最初に戻ります。 固有ベクトルの概念を示すために行列に乗算したのは、このベクトル オブジェクトでした。

ここで、λ = 12 の固有ベクトルを求めてみましょう。

• M - λ × E = -12; 4
• 6; -2.

同じ一次方程式系を作成してみましょう。

• -12x + 4y = 6x − 2y
• -18x = -6年
• 3x = y。

ここでは、x = 1 であるため、y = 3 となります。したがって、2 番目の固有ベクトルは V2 = (1; 3) のようになります。 元の行列に指定されたベクトルを乗算すると、結果は常に同じベクトルを 12 倍したものになります。これで解決アルゴリズムは終了します。 これで、行列の固有ベクトルを手動で決定する方法がわかりました。

• 決定要因。
• トレース、つまり主対角線上の要素の合計。
• ランク、つまり 最高額線形に独立した行/列。

プログラムは上記のアルゴリズムに従って動作し、解決プロセスを可能な限り短縮します。 プログラム内ではラムダが文字「c」で指定されていることを指摘することが重要です。 数値例を見てみましょう。

プログラムの動作例

次の行列の固有ベクトルを決定してみましょう。

• M = 5; 13;
• 4; 14.

これらの値を電卓のセルに入力して、次の形式で答えを取得しましょう。

• マトリックスランク: 2;
• 行列行列式: 18;
• マトリックス トレース: 19;
• 固有ベクトルの計算: c 2 − 19.00c + 18.00 (特性方程式);
• 固有ベクトル計算: 18 (最初のラムダ値);
• 固有ベクトルの計算: 1 (2 番目のラムダ値);
• ベクトル 1 の連立方程式: -13x1 + 13y1 = 4x1 − 4y1;
• ベクトル 2 の方程式系: 4x1 + 13y1 = 4x1 + 13y1;
• 固有ベクトル 1: (1; 1);
• 固有ベクトル 2: (-3.25; 1)。

したがって、2 つの線形に独立した固有ベクトルが得られました。

結論

線形代数と解析幾何学は、工学専攻の新入生にとって標準科目です。 たくさんのベクトルと行列は恐ろしいもので、このような面倒な計算では間違いを犯しやすいものです。 私たちのプログラムを使用すると、学生が自分の計算を確認したり、固有ベクトルを見つける問題を自動的に解決したりすることができます。 私たちのカタログには他にも線形代数計算機がありますので、学習や仕事に使用してください。

固有値（数値）と固有ベクトル。
解決策の例

素直になれ

両方の方程式から、次のことがわかります。

それでは、次のようにしましょう。 .

結果として： – 第 2 固有ベクトル。

繰り返しましょう 重要な点解決策:

– 結果として得られるシステムは確かに一般解を持ちます (方程式は線形に依存します)。

– 「y」が整数であり、最初の「x」座標が整数で正で可能な限り小さいように選択します。

– 特定の解がシステムの各方程式を満たすことを確認します。

答え .

中間の「チェックポイント」は十分にあったため、原則として平等性のチェックは不要です。

で さまざまな情報源情報として、固有ベクトルの座標は列ではなく行で記述されることがよくあります。次に例を示します。 （そして正直に言うと、私自身、それらを行で書き留めることに慣れています）。 このオプションは許容されますが、トピックを考慮すると 線形変換技術的にはより使いやすくなりました 列ベクトル.

おそらく解決策は非常に長く感じられたと思いますが、これは私が最初の例について詳細にコメントしたからにすぎません。

例 2

行列

自分たちでトレーニングしてみよう！ レッスンの最後の最終タスクのおおよその例。

時々行う必要があります 追加のタスク、つまり:

正準行列分解を書く

それは何ですか？

行列の固有ベクトルが次のように構成される場合 基礎の場合、次のように表すことができます。

ここで、固有ベクトルの座標で構成される行列は、 – 対角線対応する固有値を持つ行列。

この行列分解はと呼ばれます 正規のまたは 対角線.

最初の例の行列を見てみましょう。 その固有ベクトル 線形独立（非共線的）そして基礎を形成します。 それらの座標の行列を作成しましょう。

の上 主対角線行列 適切な順序で固有値が特定され、残りの要素はゼロに等しくなります。
– 順序の重要性をもう一度強調します。「2」は 1 番目のベクトルに対応するため、1 列目に配置され、「3」は 2 番目のベクトルに対応します。

通常のアルゴリズムを使用して検索する 逆行列または ガウス・ジョーダン法我々は気づく 。 いいえ、それはタイプミスではありません! - あなたが珍しい前に、のように 日食逆行列が元の行列と一致するときのイベント。

行列の正準分解を書き留める必要があります。

このシステムは次を使用して解決できます。 基本的な変換そして次の例では、 この方法。 しかし、ここでは「学校」の方法の方がはるかに速く機能します。 3 番目の方程式から次のように表現されます。 – 2 番目の方程式に代入します。

最初の座標は 0 であるため、各方程式から次の系が得られます。

そしてまた 線形関係の必須の存在に注意を払う。 自明な解しか得られない場合 の場合、固有値が間違って検出されたか、システムがコンパイル/解決されてエラーが発生しました。

コンパクトな座標が価値を与える

固有ベクトル:

そしてもう一度、解決策が見つかったことを確認します システムのすべての方程式を満たします。 以降の段落および以降のタスクでは、この願いを必須のルールとして受け入れることをお勧めします。

2) 固有値についても、同じ原理を使用して、次のシステムが得られます。

システムの 2 番目の方程式から、次のように表されます。 – 3 番目の方程式に代入します。

「ゼータ」座標はゼロに等しいため、各方程式から線形依存関係が続く系が得られます。

させて

解決策を確認する システムのすべての方程式を満たします。

したがって、固有ベクトルは次のようになります。

3) そして最後に、システムは固有値に対応します。

2 番目の式が最も単純に見えるので、これを表現して 1 番目と 3 番目の式に代入してみましょう。

すべて問題ありません。線形関係が現れました。これを次の式に代入します。

その結果、「x」と「y」は「z」で表現されました。 実際には、このような関係を正確に実現する必要はありません。場合によっては、 through または through の両方を表現する方が便利です。 または、「トレーニング」さえも可能です。たとえば、「X」から「I」、「I」から「Z」までです。

それでは、次のようにしましょう。

解決策が見つかったことを確認します システムの各方程式を満たし、3 番目の固有ベクトルを書き込みます

答え: 固有ベクトル:

幾何学的には、これらのベクトルは 3 つの異なる空間方向を定義します。 (「行ったり来たり」)、 それによれば 線形変換非ゼロベクトル (固有ベクトル) を共線ベクトルに変換します。

条件が正準分解を見つける必要がある場合、これはここで可能です。 異なる固有値は、異なる線形に独立した固有ベクトルに対応します。 マトリックスの作成 それらの座標からの対角行列 から 関連する固有値を求めて見つける 逆行列 .

条件により、次のように書く必要がある場合 固有ベクトルに基づく線形変換行列の場合は、 の形式で答えを返します。 違いはありますが、その違いは重要です。なぜなら、この行列は「de」行列だからです。

より単純な計算の問題 独立した決定:

例5

行列によって与えられる線形変換の固有ベクトルを求める

独自の数値を見つけるときは、3 次多項式まで行かないように注意してください。 さらに、あなたのシステム ソリューションは私のソリューションと異なる可能性があります。ここには確実性はありません。 また、見つかったベクトルは、それぞれの座標の比例関係までサンプル ベクトルとは異なる場合があります。 たとえば、と。 答えをフォームで提示するほうが見た目に美しいですが、2 番目の選択肢で止めても問題ありません。 ただし、すべてに合理的な制限があり、バージョンの見た目はあまりよくありません。

レッスンの最後にある課題のおおよその最終サンプル。

固有値が複数ある場合の問題をどのように解決すればよいでしょうか?

一般的なアルゴリズムは同じですが、独自の特徴があるため、ソリューションの一部をより厳格な学術スタイルに保つことをお勧めします。

例6

固有値と固有ベクトルを求める

解決

もちろん、素晴らしい最初の列を大文字にしましょう。

そして、二次三項式を因数分解した後、次のようになります。

その結果、固有値が得られ、そのうちの 2 つは倍数です。

固有ベクトルを見つけてみましょう。

1) 「単純化された」スキームに従って孤独な兵士に対処しましょう。

最後の 2 つの方程式から、等式が明確にわかります。これは明らかに、システムの最初の方程式に代入する必要があります。

これ以上良い組み合わせは見つかりません。
固有ベクトル:

2-3) 次に、いくつかの見張りを削除します。 この場合、判明する可能性があります 2つまたは1つのどちらか固有ベクトル。 根の多重度に関係なく、行列式に値を代入します。 それは私たちに次のことをもたらします 同次一次方程式系:

固有ベクトルはまさにベクトルです
解決の基本システム

実際、レッスン全体を通じて、私たちは基本的なシステムのベクトルを見つけることだけを行いました。 ただ、今のところこの用語は特に必要ありませんでした。 ところで、迷彩服を着て話題を逸した賢い学生たち 同次方程式、これから吸わされることになります。

唯一のアクションは余分な行を削除することでした。 結果は、中央に正式な「ステップ」を持つ 1 行 3 列の行列になります。
– 基本変数 – 自由変数。 したがって、自由変数は 2 つあります。 基本システムにも 2 つのベクトルがあります.

基本変数を自由変数で表現してみましょう。 「X」の前にあるゼロ乗数により、絶対に任意の値を取ることができます（これは方程式系からはっきりとわかります）。

この問題の文脈では、一般的な解決策を行ではなく列に記述する方が便利です。

このペアは固有ベクトルに対応します。
このペアは固有ベクトルに対応します。

注記 : 洗練された読者は、システムを分析するだけでこれらのベクトルを口頭で選択できます。 ただし、ここではいくつかの知識が必要です。変数が 3 つあります。 システムマトリックスランク- 1、つまり 基本的な意思決定システム 3 – 1 = 2 つのベクトルで構成されます。 ただし、検出されたベクトルは、この知識がなくても、純粋に直感的なレベルではっきりと見えます。 この場合、3 番目のベクトルはさらに「美しく」書かれます。 ただし、別の例では、単純な選択ができない可能性があるため、この条項は経験者を対象としていることに注意してください。 さらに、たとえば を 3 番目のベクトルとして取り上げてみてはいかがでしょうか。 結局のところ、その座標はシステムの各方程式とベクトルも満たします。 線形的に独立しています。 このオプションは原理的には適切ですが、「他の」ベクトルが基本システムのベクトルの線形結合であるため、「曲がった」ものになります。

答え: 固有値: 、固有ベクトル:

独立したソリューションの同様の例:

例 7

固有値と固有ベクトルを求める

レッスンの最後に、最終デザインのおおよそのサンプルが表示されます。

6 番目と 7 番目の例の両方で、線形に独立した固有ベクトルの 3 つが得られるため、元の行列が正準分解で表現できることに注意してください。 しかし、そのようなラズベリーはすべての場合に起こるわけではありません。

例8

解決: 特性方程式を作成して解いてみましょう:

最初の列の行列式を展開してみましょう。

3 次多項式を避けて、検討した方法に従ってさらに単純化を実行します。

– 固有値。

固有ベクトルを見つけてみましょう。

1) ルートには問題はありません。

驚かないでください。キットに加えて、使用されている変数もあります。ここでは違いはありません。

3 番目の方程式を式にして、1 番目と 2 番目の方程式に代入します。

両方の方程式から次のことがわかります。

それでは、次のようにしましょう。

2-3) 複数の値の場合、システムを取得します。 .

システムの行列を書き留めて、基本的な変換を使用して、それを段階的な形式にします。

「最初の部分では、ケモメトリクスを理解するために最低限必要な規定を示し、2 番目の部分では、多変量解析の方法をより深く理解するために知っておく必要がある事実が含まれています。プレゼンテーションは、Excel ワークブックで作成された例で説明されています。 マトリックス.xls、この文書に添付されています。

例へのリンクは Excel オブジェクトとしてテキスト内に配置されます。 これらの例は抽象的な性質のものであり、分析化学の問題とはまったく関係ありません。 実際の例化学測定における行列代数の使用については、さまざまな化学測定の応用をカバーする他のテキストで説明されています。

分析化学で行われる測定のほとんどは直接的なものではありませんが、 間接的な。 これは、実験では、目的の分析物 C の値 (濃度) の代わりに、別の値が取得されることを意味します。 バツ(信号)、C に関連していますが等しくない、つまり バツ(C) ≠ C. 原則として、依存の種類は バツ(C) は不明ですが、幸いなことに分析化学ではほとんどの測定値は比例します。 これは、C 濃度が増加すると、 あるつまり、信号 X は同じ量だけ増加します。 バツ(ある C) = ×(C)。 さらに、シグナルも加算的であるため、濃度 C 1 と C 2 の 2 つの物質が存在するサンプルからのシグナルは次のようになります。 合計に等しい各コンポーネントからの信号、つまり バツ(C 1 + C 2) = バツ(C1)+ バツ(C2)。 比例性と加法性を組み合わせると、 直線性。 線形性の原理を説明するために多くの例を挙げることができますが、最も重要な 2 つの例を挙げるだけで十分です。 輝く例- クロマトグラフィーと分光法。 分析化学の実験に固有の 2 番目の特徴は、 マルチチャンネル。 最新の分析機器は、多くのチャネルの信号を同時に測定します。 たとえば、光透過の強度は複数の波長で一度に測定されます。 範囲。 したがって、実験では多くの信号を扱います バツ 1 , バツ 2 ,...., バツ n、研究対象のシステム内に存在する物質の濃度セット C 1 、C 2 、...、C m を特徴付ける。

米。 1 スペクトル

したがって、分析実験は線形性と多次元性によって特徴付けられます。 したがって、実験データをベクトルと行列として考慮し、行列代数の装置を使用してそれらを操作すると便利です。 このアプローチの有益性は、4000 ～ 4796 cm -1 の 200 の波長で取得された 3 つのスペクトルを示す図に示す例で示されています。 初め （ バツ 1) と 2 番目 ( バツ 2) スペクトルは、2 つの物質 A および B の濃度が既知である標準サンプルについて取得されました。最初のサンプルでは [A] = 0.5、[B] = 0.1、2 番目のサンプルでは [A] = 0.2、[ B] = 0.6。 スペクトルが示されている新しい未知のサンプルについて何が言えるか バツ 3 ?

3 つの実験スペクトルを考えてみましょう バツ 1 , バツ 2と バツ 3 は次元 200 の 3 つのベクトルとして表されます。線形代数を使用すると、次のことを簡単に示すことができます。 バツ 3 = 0.1 バツ 1 +0.3 バツしたがって、3 番目のサンプルには明らかに物質 A と B のみが濃度 [A] = 0.5×0.1 + 0.2×0.3 = 0.11 および [B] = 0.1×0.1 + 0.6×0.3 = 0.19 で含まれています。

1. 基本情報

1.1 行列

マトリックスたとえば、長方形の数値テーブルと呼ばれます。

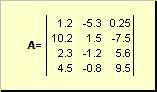
米。 2 マトリックス

行列は大文字の太字 ( あ) とその要素 - 対応する 小文字インデックス付き、つまり あるイジ。 最初のインデックスは行に番号を付け、2 番目のインデックスは列に番号を付けます。 ケモメトリクスでは、インデックスの最大値をインデックス自体と同じ文字で、ただし大文字で表すのが通例です。 したがって、行列は あ() のように書くこともできます ある ij , 私 = 1,..., 私; j = 1,..., J）。 マトリックスの例の場合 私 = 4, J= 3 そして ある 23 = −7.5.

数字のペア 私そして Jは行列の次元と呼ばれ、次のように表されます。 私× J。 ケモメトリクスにおける行列の例は、次のように取得されたスペクトルのセットです。 私のサンプル J波長。

1.2. 行列を使った最も単純な演算

行列は次のとおりです。 数値を掛ける。 この場合、各要素にこの数値が乗算されます。 例えば ​​-

米。 3 行列に数値を乗算する

同じ次元の 2 つの行列を要素ごとに指定できます 折り畳みそして 引き算。 例えば、

米。 4 マトリックスの加算

数値と加算の結果、同じ次元の行列が得られます。

ゼロ行列とは、ゼロで構成される行列です。 指定されています ○。 それは明らかです あ+○ = あ, あ−あ = ○そして0 あ = ○.

マトリックスは次のとおりです。 転置。 この操作中に、行列は反転されます。 行と列が入れ替わります。 転置はプライムで示されます。 あ"またはインデックス あ t. したがって、もし あ = {ある ij , 私 = 1,..., 私; j = 1,...,J）、 それ あ t = ( ある じ , j = 1,...,J; i = 1,..., 私）。 例えば

米。 5 マトリックス転置

それは明らかです( あ t) t = あ, (あ+B)t =A t+ B t.

1.3. 行列乗算

行列は次のとおりです。 かけるただし、適切な寸法がある場合に限ります。 なぜそうなるかは定義から明らかです。 マトリックス積 あ、 寸法 私× K、行列 B、 寸法 K× J、行列と呼ばれます C、 寸法 私× J、要素は数値です

したがって、製品に関しては AB左の行列の列数が必要です。 あ右の行列の行数と等しかった B。 マトリックス製品の例 -

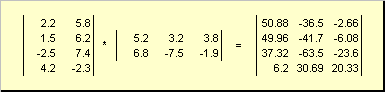
図6 行列の積

行列乗算の規則は次のように定式化できます。 行列要素を見つけるには C、交差点に立っている 私- 行目と j列目 ( c ij) は要素ごとに乗算する必要があります 私最初の行列の - 番目の行 あの上 j 2番目の行列の列目 Bそしてすべての結果を合計します。 したがって、示されている例では、3 行目と 2 列目の要素は、3 行目の要素ごとの積の合計として取得されます。 あそして2列目 B

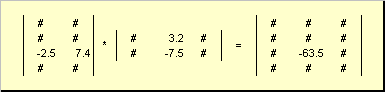
図7 行列の積の要素

行列の積は次数に依存します。 AB ≠ B.A.、少なくとも寸法上の理由から。 彼らはそれが非可換であると言います。 ただし、行列の積は結合します。 だということだ ABC = (AB)C = あ(紀元前）。 さらに、それは分配的でもあります。 あ(B+C) = AB+交流。。 それは明らかです A.O. = ○.

1.4. 正方行列

行列の列数が行数と等しい場合 ( 私 = J=N)、そのような行列は正方形と呼ばれます。 このセクションでは、そのような行列のみを考慮します。 これらの行列の中で、特別な特性を持つ行列を区別できます。

シングル行列（で示される） 私、そして時折 E) は、1 に等しい対角要素を除いて、すべての要素が 0 に等しい行列です。

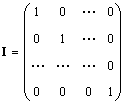
明らかに A.I. = I.A. = あ.

マトリックスはと呼ばれます 対角線、対角要素を除くすべての要素の場合 ( ある ii) はゼロに等しい。 例えば

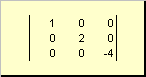
米。 8 対角行列

マトリックス あトップと呼ばれる 三角、対角線の下にあるすべての要素がゼロに等しい場合、つまり ある ij= 0、で 私>j。 例えば

米。 9 上三角行列

下三角行列も同様に定義されます。

マトリックス あ呼ばれた 対称的な、 もし あ t = あ。 言い換えると ある ij = ある じ。 例えば

米。 10 対称行列

マトリックス あ呼ばれた 直交、 もし

あ t あ = A.A. t = 私.

マトリックスはと呼ばれます 普通もし

1.5. トレースと決定要因

次正方行列 あ(Tr(で表されます) あ) または Sp( あ)) は対角要素の合計です。

例えば、

米。 11 マトリックストレース

それは明らかです

Sp(α あ) = α Sp( あ） そして

Sp( あ+B) = Sp( あ)+Sp( B).

それは次のことを示すことができます

Sp( あ) = Sp( あ t)、Sp( 私) = N,

そしてそれも

Sp( AB) = Sp( B.A.).

別の 重要な特性正方行列はその 決定要因(det(と表記) あ））。 一般的な場合に行列式を決定することは非常に難しいため、最も単純なオプションである行列から始めます。 あ寸法 (2×2)。 それから

(3×3) 行列の場合、行列式は次と等しくなります。

マトリックスの場合 ( N× N) 行列式は合計 1・2・3・ ... ・として計算されます。 N= N！ それぞれの項が等しい

インデックス k 1 , k 2 ,..., kN可能なすべての順序付けされた置換として定義されます rセット内の数値 (1、2、...、 N）。 行列の行列式の計算は複雑な手順であり、実際には特別なプログラムを使用して実行されます。 例えば、

米。 12 行列行列式

明白な特性だけをメモしておきます。

デット( 私) = 1、det( あ) = det( あ t)、

デット( AB) = det( あ)デット( B).

1.6. ベクトル

行列が 1 列のみで構成されている場合 ( J= 1) の場合、そのようなオブジェクトが呼び出されます。 ベクター。 より正確には、列ベクトルです。 例えば

たとえば、1 つの行で構成される行列を考慮することもできます。

このオブジェクトもベクトルですが、 行ベクトル。 データを分析するときは、列と行のどちらのベクトルを扱っているのかを理解することが重要です。 したがって、1 つのサンプルから取得されたスペクトルは行ベクトルとして考えることができます。 次に、すべてのサンプルの特定の波長におけるスペクトル強度のセットを列ベクトルとして扱う必要があります。

ベクトルの次元は、その要素の数です。

転置によって任意の列ベクトルを行ベクトルに変換できることは明らかです。

ベクトルの形状を特に述べず、単にベクトルという場合は、列ベクトルを意味する。 私たちもこのルールを遵守します。 ベクトルは、小文字の順方向の太字で表されます。 ゼロ ベクトルとは、すべての要素がゼロであるベクトルです。 指定されています 0 .

1.7. ベクトルを使った最も単純な演算

ベクトルは、行列と同じ方法で加算したり数値を乗算したりできます。 例えば、

米。 13 ベクトルを使った演算

2 つのベクトル バツそして y呼ばれます 同一直線上にある、次のような数 α がある場合、

1.8. ベクトルの積

同じ次元の 2 つのベクトル N乗算することができます。 ベクトルが 2 つあるとします バツ = (バツ 1 , バツ 2 ,...,バツ N)tと y = (y 1 , y 2 ,...,y N) t 。 行と列の乗算ルールに従って、それらから 2 つの積を構成できます。 バツ t yそして xy t. 最初の作品

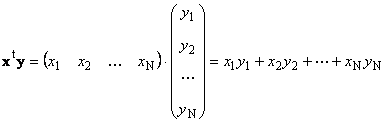
呼ばれた スカラーまたは 内部。 その結果は数値です。 () で表されることもあります。 バツ,y)= バツ t y。 例えば、

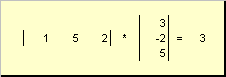
米。 14 内積（スカラー）

2枚目

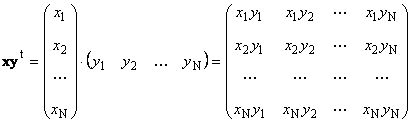
呼ばれた 外部の。 その結果は次の次元の行列になります ( N× N）。 例えば、

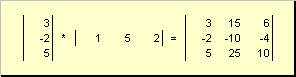
米。 15 外部業務

スカラー積がゼロであるベクトルを次のように呼びます。 直交.

1.9. ベクトルノルム

ベクトルとそれ自体のスカラー積は、スカラー二乗と呼ばれます。 この値

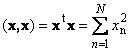
正方形を定義します 長さベクター バツ。 長さを示すため（とも呼ばれます） 標準ベクトル）表記が使用されます

例えば、

米。 16 ベクトルノルム

単位長ベクトル (|| バツ|| = 1) は正規化と呼ばれます。 ゼロ以外のベクトル ( バツ ≠ 0 ) は、長さで割ることによって正規化できます。 バツ = ||バツ|| (バツ/||バツ||) = ||バツ|| e。 ここ e = バツ/||バツ|| - 正規化されたベクトル。

ベクトルがすべて正規化され、ペアごとに直交している場合、ベクトルは正規直交と呼ばれます。

1.10. ベクトル間の角度

スカラー積により次のことが決定され、 コーナー 2 つのベクトル間の φ バツそして y

ベクトルが直交している場合は、cosφ = 0 および φ = π/2 であり、同一直線上にある場合は、cosφ = 1 および φ = 0 です。

1.11. 行列のベクトル表現

各マトリクス あサイズ 私× Jベクトルの集合として表現できる

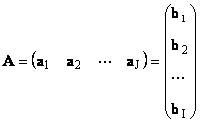
ここですべてのベクトル ある jは j番目の列と行ベクトル b 私は 私行列の 2 行目 あ

1.12. 線形依存ベクトル

同じ次元のベクトル ( N) は、行列と同様に、数値を加算したり乗算したりできます。 結果は同じ次元のベクトルになります。 同じ次元のベクトルがいくつかあるとします。 バツ 1 , バツ 2 ,...,バツ K と同じ数の数 α α 1 , α 2 ,...,α K。 ベクター

y= α 1 バツ 1+α2 バツ 2+...+α K バツ K

呼ばれた 線形結合ベクトル バツ k .

このようなゼロ以外の数 α が存在する場合 k ≠ 0, k = 1,..., K、 何 y = 0 、そのようなベクトルのセット バツ k呼ばれた 線形依存性。 それ以外の場合、ベクトルは線形独立であると呼ばれます。 たとえば、ベクトル バツ 1 = (2, 2) t および バツ 2 = (−1, −1) t は線形従属です。 バツ 1 +2バツ 2 = 0

1.13。 マトリックスランク

のセットを考えてみましょう Kベクトル バツ 1 , バツ 2 ,...,バツ K寸法 N。 このベクトル系のランクは、線形独立ベクトルの最大数です。 たとえばセットでは

たとえば、線形に独立したベクトルは 2 つだけです。 バツ 1と バツ 2なのでランクは2です。

明らかに、セット内にその次元 ( K>N) の場合、それらは必然的に線形依存します。

マトリックスランク(ランク(で示されます) あ)) は、それを構成するベクトル系のランクです。 どの行列も 2 つの方法 (列ベクトルまたは行ベクトル) で表現できますが、これはランク値には影響しません。

1.14。 逆行列

正方行列 あ一意の属性を持つ場合、非縮退と呼ばれます。 逆行するマトリックス あ-1、条件により決定

A.A. −1 = あ −1 あ = 私.

逆行列はすべての行列に存在するわけではありません。 非縮退の必要十分条件は、

デット( あ) ≠ 0 またはランク( あ) = N.

逆行列は複雑な手順であり、特別なプログラムが必要です。 例えば、

米。 17 逆行列

最も単純なケース、つまり 2×2 行列の式を示しましょう。

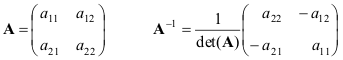
行列の場合 あそして B非退化である場合、

(AB) −1 = B −1 あ −1 .

1.15。 擬似逆行列

マトリックスの場合 あ退化して 逆行列存在しない場合は、場合によっては使用できます 擬似逆行列、そのような行列として定義されます あ+それ

A.A. + あ = あ.

擬似逆行列は唯一のものではなく、その形式は構築方法によって異なります。 たとえば、長方形行列の場合は、ムーア・ペンローズ法を使用できます。

列数の場合 少ない数行、その後

あ + =(あ t あ) −1 あ t

例えば、

米。 17a 行列の擬似逆行列

列数の場合 さらに多くの数行、その後

あ + =あ t ( A.A.と） −1

1.16 ベクトルと行列の乗算

ベクター バツ行列を掛けることができます あ適切なサイズ。 この場合、列ベクトルは右側で乗算されます。 斧、ベクトル行は左側にあります バツ t あ。 ベクトル次元の場合 J、行列の次元 私× J結果は次元のベクトルになります 私。 例えば、

米。 18 ベクトルと行列の乗算

マトリックスの場合 あ- 四角 （ 私× 私)、次にベクトル y = 斧と同じ次元を持っています バツ。 それは明らかです

あ(α1 バツ 1+α2 バツ 2) = α 1 斧 1+α2 斧 2 .

したがって、行列はベクトルの線形変換と考えることができます。 特に イクス = バツ, 牛 = 0 .

2. 追加情報

2.1. 連立一次方程式

させて あ- マトリックスのサイズ 私× J、A b- 次元ベクトル J。 方程式を考えてみましょう

斧 = b

ベクトルに対して バツ、寸法 私。 本質的には、次のようなシステムです。 私との一次方程式 J未知 バツ 1 ,...,バツ J。 解決策は次の場合にのみ存在します。

ランク( あ) = ランク( B) = R,

どこ B次元の拡張行列です 私×( J+1)、行列で構成されます あ、コラムで補足 b, B = (あ b）。 そうしないと、方程式に矛盾が生じます。

もし R = 私 = Jの場合、解決策はユニークです

バツ = あ −1 b.

もし R < 私、それならたくさんあります さまざまなソリューション、線形結合で表現できます。 J−Rベクトル。 同次方程式系 斧 = 0 正方行列付き あ (N× N) には自明ではない解決策があります ( バツ ≠ 0 ) det( あ) = 0。 R= ランク( あ)<N、それから、 N−R線形に独立した解。

2.2. 双一次形式と二次形式

もし あは正方行列であり、 バツそして y- 対応する次元のベクトル、その後の形式のスカラー積 バツ t ああ呼ばれた 双線形行列で定義された形式 あ。 で バツ = y表現 バツ t 斧呼ばれた 二次関数形状。

2.3. 正定行列

正方行列 あ呼ばれた 正定値、ゼロ以外のベクトルの場合 バツ ≠ 0 ,

バツ t 斧 > 0.

同様に定義される ネガティブ (バツ t 斧 < 0), 非負 (バツ t 斧≥ 0) および ネガティブ (バツ t 斧≤ 0) 特定の行列。

2.4. コレスキー分解

対称行列の場合 あが正定値である場合、一意の三角行列が存在します。 Uポジティブな要素が含まれているため、

あ = U t U.

例えば、

米。 19 コレスキー分解

2.5. 極性分解

させて あ次元の非特異正方行列です N× N。 それからユニークなものがあります 極地パフォーマンス

あ = S.R.

どこ Sは非負の対称行列であり、 Rは直交行列です。 行列 Sそして R明示的に定義できます。

S 2 = A.A.または S = (A.A. t) 1/2と R = S −1 あ = (A.A. t) −1/2 あ.

例えば、

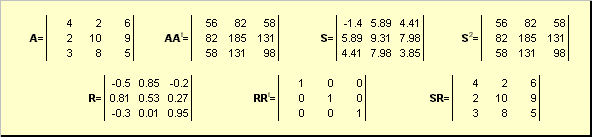
米。 20 極性分解

マトリックスの場合 あが縮退している場合、分解は一意ではありません。つまり、次のようになります。 Sまだ一人だけど、 Rたぶんたくさん。 極分解は行列を表します あ圧縮/拡張の組み合わせとして Sそして向きを変える R.

2.6. 固有ベクトルと固有値

させて あは正方行列です。 ベクター v呼ばれた 固有ベクトル行列 あ、 もし

平均 = λ v,

ここで、数値 λ は次のように呼ばれます。 固有値行列 あ。 したがって、行列が実行する変換は あベクトルの上に v、係数 λ による単純な伸長または圧縮になります。 固有ベクトルは、定数 α ≠ 0 を乗算するまで決定されます。 もし vは固有ベクトル、その後 α v- 固有ベクトルでもあります。

2.7. 固有値

マトリックスで あ、 寸法 （ N× N) を超えることはできません N固有値。 彼らは満足します 特性方程式

デット( あ − λ 私) = 0,

いる 代数方程式 N-番目の注文。 特に、2×2 行列の場合、特性方程式は次の形式になります。

例えば、

米。 21 固有値

固有値のセット λ 1 ,..., λ N行列 あ呼ばれた スペクトラム あ.

スペクトルにはさまざまな性質があります。 特に

デット( あ) = λ 1 ×...×λ N,Sp( あ) = λ 1 +...+λ N.

任意の行列の固有値は複素数にすることができますが、行列が対称であれば ( あ t = あ) の場合、その固有値は実数になります。

2.8. 固有ベクトル

マトリックスで あ、 寸法 （ N× N) を超えることはできません N固有ベクトル。それぞれが独自の固有値に対応します。 固有ベクトルを決定するには v n等次方程式系を解く必要がある

(あ − λ n 私)v n = 0 .

det( A −λ n 私) = 0.

例えば、

米。 22 固有ベクトル

対称行列の固有ベクトルは直交します。