この記事では、あらゆる種類の問題を分析して見つけます。

覚えておきましょう 導関数の幾何学的意味: 接線が関数のグラフの点に描かれている場合、接線の傾き係数 (接線と軸の正の方向との間の角度の正接に等しい) は関数の導関数に等しくなります。という時点で。

接線上の任意の点を座標で取ってみましょう。

そして、直角三角形を考えてみましょう。

この三角形の中で

ここから

これは、その点で関数のグラフに引かれた接線の方程式です。

接線の方程式を書くには、関数の方程式と接線が引かれる点を知るだけで済みます。 次に、 と を見つけることができます。

接線方程式の問題には主に 3 つのタイプがあります。

1. 連絡先の指定

2. 接線の傾き係数、つまり、その点における関数の導関数の値が与えられます。

3. 接線が引かれる点の座標が指定されていますが、接線の点ではありません。

それぞれのタスクの種類を見てみましょう。

1. 関数のグラフに接線の方程式を書きます 時点で .

.

b) 点 における導関数の値を求めます。 まず関数の導関数を求めましょう

見つかった値を接線方程式に代入してみましょう。

方程式の右側の括弧を開いてみましょう。 我々が得る：

答え： .

2. 関数がグラフに接する点の横座標を求めます。 x 軸に平行です。

接線が x 軸に平行な場合、接線と軸の正の方向の間の角度は次のようになります。 ゼロに等しいしたがって、接線角度の正接はゼロになります。 これは、関数の導関数の値が 接触点ではゼロになります。

a) 関数の導関数を求めます。 .

b) 導関数をゼロとみなして、接線が軸に平行になる値を見つけてみましょう。

各係数をゼロにすると、次のようになります。

答え: 0;3;5

3. 関数のグラフへの接線の方程式を書く , 平行 真っ直ぐ .

接線は線と平行です。 この線の傾きは -1 です。 したがって、接線はこの線に平行であるため、接線の傾きも -1 になります。 あれは 私たちは接線の傾きを知っています、 それによって、 接点における微分値.

これは、接線方程式を求める 2 番目のタイプの問題です。

したがって、接点における導関数の関数と値が与えられます。

a) 関数の導関数が -1 に等しい点を見つけます。

まず、微分方程式を求めます。

導関数を数値 -1 とみなします。

その点での関数の値を求めてみましょう。

(条件による)

.

b) 点 における関数のグラフの接線の方程式を求めます。

その点での関数の値を求めてみましょう。

(条件による)。

これらの値を接線方程式に代入してみましょう。

.

答え：

４． 曲線の接線の方程式を書きます , 点を通過する

まず、その点が接点であるかどうかを確認してみましょう。 点が接点の場合、その点は関数のグラフに属し、その座標は関数の方程式を満たさなければなりません。 関数の方程式に点の座標を代入してみましょう。

Title="1sqrt(8-3^2)">. Мы получили под корнем отрицательное число, равенство не верно, и точка не принадлежит графику функции и !} 連絡先ではありません。

これは、接線方程式を求める最後のタイプの問題です。 初めにすること 接点の横座標を見つける必要があります.

値を見つけてみましょう。

連絡窓口とさせていただきます。 点は関数のグラフの接線に属します。 この点の座標を接線方程式に代入すると、正しい等式が得られます。

.

ある点における関数の値は次のとおりです。 .

その点における関数の導関数の値を求めてみましょう。

まず、関数の導関数を求めます。 これ 。

ある点での導関数は次の値に等しい .

と の式を接線方程式に代入してみましょう。 次の方程式が得られます。

この方程式を解いてみましょう。

分数の分子と分母を 2 で減らします。

方程式の右辺を次のように簡略化してみましょう 共通点。 我々が得る：

分数の分子を単純化し、両辺を乗算してみましょう。この式は厳密にゼロより大きくなります。

方程式が得られます

解決しましょう。 これを行うには、両方の部分を二乗して、システムに進みましょう。

Title="delim(lbrace)(matrix(2)(1)((64-48(x_0)+9(x_0)^2=8-(x_0)^2) (8-3x_0>=0) )))( )">!}

最初の方程式を解いてみましょう。

決めましょう 二次方程式、 我々が得る

2 番目のルートは条件 title="8-3x_0>=0) を満たしていません">, следовательно, у нас только одна точка касания и её абсцисса равна .!}

その点における曲線の接線の方程式を書いてみましょう。 これを行うには、式に値を代入します。 - すでに録音しました。

答え：
.

の上 現代の舞台教育の発展において、その主な任務の一つは、創造的に考える人格の形成です。 学生の創造力は、体系的に基礎を学ぶ場合にのみ開発できます。 研究活動。 学生が創造力、能力、才能を発揮するための基礎は、本格的な知識とスキルを形成します。 この点で、学校数学の科目ごとに基礎的な知識と技能の体系を形成するという問題は決して重要ではない。 同時に、本格的なスキルは、個々のタスクではなく、注意深く考え抜かれたそれらのシステムの教訓的な目標である必要があります。 最も広い意味では、システムは、完全性と安定した構造を備えた相互接続された相互作用する要素のセットとして理解されます。

関数のグラフの接線の方程式の書き方を生徒に教えるための手法を考えてみましょう。 基本的に、接方程式を見つける際のすべての問題は、線のセット (バンドル、ファミリー) から、特定の要件を満たす線、つまり特定の関数のグラフに接する線を選択する必要性に帰着します。 この場合、選択が実行される行のセットは 2 つの方法で指定できます。

a) xOy 平面上にある点 (中央の鉛筆)。
b) 角度係数 (平行な直線ビーム)。

これに関して、システムの要素を分離するために「関数のグラフへの接線」というトピックを研究したときに、次の 2 種類の問題を特定しました。

1) 通過する点によって与えられる接線に関する問題。
2) 傾きによって与えられる接線に関する問題。

接線問題を解くトレーニングは、A.G. が提案したアルゴリズムを使用して実施されました。 モルドコビッチ。 すでに知られているものとの基本的な違いは、接点の横座標が (x0 ではなく) 文字 a で示されるため、接線の方程式は次の形式をとることです。

y = f(a) + f "(a)(x – a)

(y = f(x 0) + f "(x 0)(x – x 0) と比較してください。) この方法論的手法により、学生は現在の点の座標がどこに書かれているかを迅速かつ簡単に理解できるようになります。一般的な接線方程式、および接点はどこにありますか。

関数 y = f(x) のグラフに対する接線方程式を作成するアルゴリズム

1. 接点の横座標を文字 a で指定します。
2. f(a) を求めます。
3. f "(x) と f "(a) を求めます。
4. 見つかった数値 a、f(a)、f "(a) を代入します。 一般方程式タンジェント y = f(a) = f "(a)(x – a)。

このアルゴリズムは、生徒が独自に特定した操作とその実装順序に基づいてコンパイルできます。

実践がそれを示しています 逐次解決策アルゴリズムの助けを借りた各主要なタスクにより、関数のグラフへの接線の方程式を段階的に書くスキルを開発することができ、アルゴリズムのステップはアクションの基準点として機能します。 このアプローチは、P.Yaによって開発された精神的行動の段階的な形成の理論に対応しています。 ガルペリンと N.F. タリジナ。

最初のタイプのタスクでは、2 つの重要なタスクが特定されました。

• 接線は曲線上の点を通過します (問題 1)。
• 接線は曲線上にない点を通過します (問題 2)。

タスク 1. 関数のグラフの接線の方程式を書きます。 点 M(3; – 2) で。

解決。 点 M(3; – 2) は接点です。

1. a = 3 – 接点の横座標。
2. f(3) = – 2.
3. f "(x) = x 2 – 4、f "(3) = 5。
y = – 2 + 5(x – 3)、y = 5x – 17 – 接線方程式。

問題 2. 点 M(- 3; 6) を通る関数 y = – x 2 – 4x + 2 のグラフのすべての接線の方程式を書きなさい。

解決。 f(- 3) 6 (図 2) であるため、点 M(- 3; 6) は接点ではありません。

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4、f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – 接線方程式。

接線は点 M(- 3; 6) を通過するため、その座標は接線方程式を満たします。

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a)、
a 2 + 6a + 8 = 0 ^ a 1 = – 4、a 2 = – 2。

a = – 4 の場合、接線方程式は y = 4x + 18 となります。

a = – 2 の場合、接線方程式は y = 6 の形式になります。

2 番目のタイプでは、主なタスクは次のとおりです。

• 接線はある線と平行です (問題 3)。
• 接線は指定された線に対して特定の角度で通過します (問題 4)。

問題 3. 関数 y = x 3 – 3x 2 + 3 のグラフのすべての接線の方程式を、直線 y = 9x + 1 に平行に書きなさい。

1. a – 接点の横座標。
2. f(a) = a 3 – 3a 2 + 3。
3. f "(x) = 3x 2 – 6x、f "(a) = 3a 2 – 6a.

しかし、一方で f "(a) = 9 (並列条件) です。これは、方程式 3a 2 – 6a = 9 を解く必要があることを意味します。その根は a = – 1、a = 3 です (図 3) ）。

4. 1) a = – 1;
2) f(-1) = -1;
3) f "(-1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – 接線方程式;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – 接線方程式。

問題 4. 直線 y = 0 に対して 45°の角度で通る関数 y = 0.5x 2 – 3x + 1 のグラフへの接線の方程式を書きなさい (図 4)。

解決。 条件 f "(a) = Tan 45° から、a: a – 3 = 1 ^ a = 4 が求められます。

1. a = 4 – 接点の横座標。
2. f(4) = 8 – 12 + 1 = – 3。
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4)。

y = x – 7 – 接線方程式。

他の問題を解決するには、結局 1 つ以上の重要な問題を解決する必要があることを示すのは簡単です。 例として次の 2 つの問題を考えてみましょう。

1. 接線が直角に交差し、接線の 1 つが横軸 3 の点で放物線に接する場合、放物線の接線の方程式を書きます (図 5)。

解決。 接点の横座標が与えられているため、解法の最初の部分は重要な問題 1 に要約されます。

1. a = 3 – いずれかの辺の接点の横座標 直角.
2. f(3) = 1。
3. f "(x) = 4x – 5、f "(3) = 7。
4. y = 1 + 7(x – 3)、y = 7x – 20 – 最初の接線の方程式。

最初の接線の傾斜角を a とします。 接線は垂直なので、 は 2 番目の接線の傾斜角になります。 最初の接線の方程式 y = 7x – 20 から、tg a = 7 が得られます。

これは、2 番目の接線の傾きが に等しいことを意味します。

さらなる解決策は重要なタスク 3 になります。

B(c; f(c)) を 2 番目の線の接点とすると、次のようになります。

1. – 2 番目の接点の横座標。
2.
3.
4.
– 2 番目の接線の方程式。

注記。 生徒が垂線の係数の比 k 1 k 2 = – 1 を知っていれば、接線の角度係数をより簡単に見つけることができます。

2. 関数のグラフに共通するすべての接線の方程式を書きます。

解決。 問題は、共通接線の接点の横座標を見つけること、つまり、次の重要な問題 1 を解決することになります。 一般的な見解、連立方程式とその後の解法を作成します (図 6)。

1. 関数 y = x 2 + x + 1 のグラフ上にある接点の横座標を a とします。
2. f(a) = a 2 + a + 1。
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 。

1. c を関数のグラフ上の接点の横座標とします。
2.
3. f "(c) = c.
4.

接線は一般的なので、

したがって、y = x + 1 と y = – 3x – 3 は共通接線です。

検討されたタスクの主な目的は、学生がさらに多くの問題を解決する際に、重要な問題の種類を自主的に認識できるようにすることです。 複雑なタスク、特定の研究スキル（分析、比較、一般化、仮説の提示などの能力）が必要です。 このようなタスクには、キー タスクがコンポーネントとして含まれるあらゆるタスクが含まれます。 例として、接線の族から関数を見つけるという問題 (問題 1 の逆) を考えてみましょう。

3. 関数 y = x 2 + bx + c のグラフに接する線 y = x および y = – 2x は、どの b および c ですか?

直線 y = x と放物線 y = x 2 + bx + c の接点の横座標を t とします。 p は、直線 y = – 2x と放物線 y = x 2 + bx + c の接点の横座標です。 この場合、接線方程式 y = x は y = (2t + b)x + c – t 2 の形式になり、接線方程式 y = – 2x は y = (2p + b)x + c – p 2 の形式になります。 。

連立方程式を作って解いてみましょう

答え：

関数のグラフの接線の方程式

P.ロマノフ、T.ロマノバ、
マグニトゴルスク、
チェリャビンスク地方

関数のグラフの接線の方程式

この記事はITAKA+ホテルコンプレックスの協力を得て掲載されました。 造船業の街セヴェロドビンスクに滞在する場合、仮住まいを見つけるという問題に遭遇することはありません。 、ホテル複合施設「ITHAKA+」のウェブサイト http://itakaplus.ru では、市内のアパートを任意の期間、日払いで簡単かつ迅速に借りることができます。

教育の発展の現段階では、その主な課題の一つは、創造的に考える人格の形成です。 学生の創造力は、研究活動の基礎を体系的に取り組んでこそ育まれます。 学生が創造力、能力、才能を発揮するための基礎は、本格的な知識とスキルを形成します。 この点で、学校数学の科目ごとに基礎的な知識と技能の体系を形成するという問題は決して重要ではない。 同時に、本格的なスキルは、個々のタスクではなく、注意深く考え抜かれたそれらのシステムの教訓的な目標である必要があります。 最も広い意味では、システムは、完全性と安定した構造を備えた相互接続された相互作用する要素のセットとして理解されます。

関数のグラフの接線の方程式の書き方を生徒に教えるための手法を考えてみましょう。 基本的に、接線方程式を見つけるすべての問題は、線のセット (バンドル、ファミリー) から特定の要件を満たす線、つまり特定の関数のグラフに接する線を選択する必要性に帰着します。 この場合、選択が実行される行のセットは 2 つの方法で指定できます。

a) xOy 平面上にある点 (中央の鉛筆)。
b) 角度係数 (平行な直線ビーム)。

これに関して、システムの要素を分離するために「関数のグラフへの接線」というトピックを研究したとき、次の 2 種類の問題が特定されました。

1) 通過する点によって与えられる接線に関する問題。
2) 傾きによって与えられる接線に関する問題。

接線問題を解くトレーニングは、A.G. が提案したアルゴリズムを使用して実施されました。 モルドコビッチ。 すでに知られているものとの基本的な違いは、接点の横座標が (x0 ではなく) 文字 a で示されるため、接線の方程式は次の形式をとることです。

y = f(a) + f "(a)(x – a)

(y = f(x 0) + f "(x 0)(x – x 0) と比較してください。) この方法論的手法により、学生は現在の点の座標がどこに書かれているかを迅速かつ簡単に理解できるようになります。一般的な接線方程式、および接点はどこにありますか。

関数 y = f(x) のグラフに対する接線方程式を作成するアルゴリズム

1. 接点の横座標を文字 a で指定します。
2. f(a) を求めます。
3. f "(x) と f "(a) を求めます。
4. 見つかった数値 a、f(a)、f "(a) を一般接線方程式 y = f(a) = f "(a)(x – a) に代入します。

このアルゴリズムは、生徒が独自に特定した操作とその実装順序に基づいてコンパイルできます。

実践の結果、アルゴリズムを使用して主要な問題のそれぞれを順番に解決することで、関数のグラフの接線の方程式を段階的に書くスキルを身につけることができ、アルゴリズムのステップがアクションの基準点として機能することがわかりました。 。 このアプローチは、P.Yaによって開発された精神的行動の段階的な形成の理論に対応しています。 ガルペリンと N.F. タリジナ。

最初のタイプのタスクでは、2 つの重要なタスクが特定されました。

• 接線は曲線上の点を通過します (問題 1)。
• 接線は曲線上にない点を通過します (問題 2)。

タスク 1. 関数のグラフの接線の方程式を書きます。 点 M(3; – 2) で。

解決。 点 M(3; – 2) は接点です。

1. a = 3 – 接点の横座標。
2. f(3) = – 2.
3. f "(x) = x 2 – 4、f "(3) = 5。
y = – 2 + 5(x – 3)、y = 5x – 17 – 接線方程式。

問題 2. 点 M(- 3; 6) を通る関数 y = – x 2 – 4x + 2 のグラフのすべての接線の方程式を書きなさい。

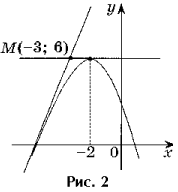解決。 f(- 3) であるため、点 M(- 3; 6) は接点ではありません。６（図２）。

2. f(a) = – a 2 – 4a + 2.
3. f "(x) = – 2x – 4、f "(a) = – 2a – 4.
4. y = – a 2 – 4a + 2 – 2(a + 2)(x – a) – 接線方程式。

接線は点 M(- 3; 6) を通過するため、その座標は接線方程式を満たします。

6 = – a 2 – 4a + 2 – 2(a + 2)(– 3 – a)、
a 2 + 6a + 8 = 0^ a 1 = – 4、a 2 = – 2。

a = – 4 の場合、接線方程式は y = 4x + 18 となります。

a = – 2 の場合、接線方程式は y = 6 の形式になります。

2 番目のタイプでは、主なタスクは次のとおりです。

• 接線はある線と平行です (問題 3)。
• 接線は指定された線に対して特定の角度で通過します (問題 4)。

問題 3. 関数 y = x 3 – 3x 2 + 3 のグラフのすべての接線の方程式を、直線 y = 9x + 1 に平行に書きなさい。

解決。

1. a – 接点の横座標。
2. f(a) = a 3 – 3a 2 + 3。
3. f "(x) = 3x 2 – 6x、f "(a) = 3a 2 – 6a.

しかし、一方で f "(a) = 9 (並列条件) です。これは、方程式 3a 2 – 6a = 9 を解く必要があることを意味します。その根は a = – 1、a = 3 です (図 3) ）。

4. 1) a = – 1;
2) f(-1) = -1;
3) f "(-1) = 9;
4) y = – 1 + 9(x + 1);

y = 9x + 8 – 接線方程式;

1) a = 3;
2) f(3) = 3;
3) f "(3) = 9;
4) y = 3 + 9(x – 3);

y = 9x – 24 – 接線方程式。

問題 4. 直線 y = 0 に対して 45°の角度で通る関数 y = 0.5x 2 – 3x + 1 のグラフへの接線の方程式を書きなさい (図 4)。

解決。 条件 f "(a) = Tan 45° から、a がわかります: a – 3 = 1^a = 4。

1. a = 4 – 接点の横座標。
2. f(4) = 8 – 12 + 1 = – 3。
3. f "(4) = 4 – 3 = 1.
4. y = – 3 + 1(x – 4)。

y = x – 7 – 接線方程式。

他の問題を解決するには、結局 1 つ以上の重要な問題を解決する必要があることを示すのは簡単です。 例として次の 2 つの問題を考えてみましょう。

1. 接線が直角に交差し、接線の 1 つが横軸 3 の点で放物線に接する場合、放物線の接線の方程式を書きます (図 5)。

解決。 接点の横座標が与えられているため、解法の最初の部分は重要な問題 1 に要約されます。

1. a = 3 – 直角のいずれかの辺の接点の横座標。
2. f(3) = 1。
3. f "(x) = 4x – 5、f "(3) = 7。
4. y = 1 + 7(x – 3)、y = 7x – 20 – 最初の接線の方程式。

しましょう – 最初の接線の傾斜角度。 接線は垂直なので、 は 2 番目の接線の傾斜角になります。 最初の接線の方程式 y = 7x – 20 から、tg が得られます。 a = 7. 見つけてみましょう

これは、2 番目の接線の傾きが に等しいことを意味します。

さらなる解決策は重要なタスク 3 になります。

B(c; f(c)) を 2 番目の線の接点とすると、次のようになります。

1. – 2 番目の接点の横座標。
2.
3.
4.
– 2 番目の接線の方程式。

注記。 生徒が垂線の係数の比 k 1 k 2 = – 1 を知っていれば、接線の角度係数をより簡単に見つけることができます。

2. 関数のグラフに共通するすべての接線の方程式を書きます。

解決。 課題は、共通接線の接点の横座標を見つけること、つまり、主要な問題 1 を一般形式で解き、連立方程式を作成してそれを解くことになります (図 6)。

1. 関数 y = x 2 + x + 1 のグラフ上にある接点の横座標を a とします。
2. f(a) = a 2 + a + 1。
3. f "(a) = 2a + 1.
4. y = a 2 + a + 1 + (2a + 1)(x – a) = (2a + 1)x + 1 – a 2 。

1. c を関数のグラフ上の接点の横座標とします。
2.
3. f "(c) = c.
4.

接線は一般的なので、

したがって、y = x + 1 と y = – 3x – 3 は共通接線です。

検討された課題の主な目的は、特定の研究スキル (分析、比較、一般化、仮説の提案などの能力) を必要とする、より複雑な問題を解決する際に、学生が主体的に重要な問題の種類を認識できるようにすることです。 このようなタスクには、キー タスクがコンポーネントとして含まれるあらゆるタスクが含まれます。 例として、接線の族から関数を見つけるという問題 (問題 1 の逆) を考えてみましょう。

3. 関数 y = x 2 + bx + c のグラフに接する線 y = x および y = – 2x は、どの b および c ですか?

解決。

直線 y = x と放物線 y = x 2 + bx + c の接点の横座標を t とします。 p は、直線 y = – 2x と放物線 y = x 2 + bx + c の接点の横座標です。 この場合、接線方程式 y = x は y = (2t + b)x + c – t 2 の形式になり、接線方程式 y = – 2x は y = (2p + b)x + c – p 2 の形式になります。 。

連立方程式を作って解いてみましょう

答え：

自主的に解決すべき問題

1. 関数 y = 2x 2 – 4x + 3 のグラフと直線 y = x + 3 の交点に引かれる接線の方程式を書きます。

答え: y = – 4x + 3、y = 6x – 9.5。

2. 横軸 x 0 = 1 のグラフの点で関数 y = x 2 – ax のグラフに引かれた接線は点 M(2; 3) を通過しますか?

答え: a = 0.5。

3. p のどの値の場合、直線 y = px – 5 は曲線 y = 3x 2 – 4x – 2 に接触しますか?

答え: p 1 = – 10、p 2 = 2。

4. 関数 y = 3x – x 3 のグラフのすべての共通点と、点 P(0; 16) を通ってこのグラフに引かれた接線を見つけます。

答え: A(2; – 2)、B(– 4; 52)。

5. 放物線 y = x 2 + 6x + 10 と直線の間の最短距離を見つけます。

答え：

6. 曲線 y = x 2 – x + 1 上で、グラフの接線が直線 y – 3x + 1 = 0 と平行になる点を見つけます。

答え: M(2; 3)。

7. 関数 y = x 2 + 2x – | のグラフの接線の方程式を書きます。 4x |、2 点で接触します。 図面を作成します。

答え: y = 2x – 4。

8. 直線 y = 2x – 1 が曲線 y = x 4 + 3x 2 + 2x と交差しないことを証明します。 それらの最も近い点の間の距離を見つけます。

答え：

9. 放物線 y = x 2 上で、横座標 x 1 = 1、x 2 = 3 の 2 つの点が取られます。これらの点を通る割線が引かれます。 放物線のどの点でその接線が正割線と平行になるでしょうか? セカントとタンジェントの方程式を書きます。

答え: y = 4x – 3 – セカント方程式。 y = 4x – 4 – 接線方程式。

10.角度qを求めます 関数 y = x 3 – 4x 2 + 3x + 1 のグラフの接線間の、横軸 0 と 1 の点で描かれたもの。

答え: q = 45°。

11. 関数のグラフの接線が Ox 軸と 135° の角度を形成する点は何ですか?

答え: A(0; – 1)、B(4; 3)。

12. 曲線の点 A(1; 8) で 接線が引かれます。 座標軸間の接線の長さを求めます。

答え：

13. 関数 y = x 2 – x + 1 および y = 2x 2 – x + 0.5 のグラフに対するすべての共通接線の方程式を書きます。

答え: y = – 3x および y = x。

14. 関数のグラフの接線間の距離を求めます x 軸に平行です。

答え：

15. 放物線 y = x 2 + 2x – 8 が x 軸と交差する角度を決定します。

答え: q 1 = arctan 6、q 2 = arctan (- 6)。

16. 関数グラフ すべての点を検索します。このグラフの各接線が座標の正の半軸と交差し、それらから等しいセグメントを切り取ります。

答え: A(- 3; 11)。

17. 直線 y = 2x + 7 と放物線 y = x 2 – 1 は点 M と N で交差します。点 M と N で放物線に接する線の交点 K を求めます。

答え: K(1; – 9)。

18. 関数 y = x 3 – 3x + 15 のグラフに接する線 y = 9x + b は、b のどの値に対して成りますか?

答え: – 1; 31.

19. k の値について、直線 y = kx – 10 は 1 つだけ存在しますか 共通点関数 y = 2x 2 + 3x – 2 のグラフでは? 見つかった k の値に対して、点の座標を決定します。

答え: k 1 = – 5, A(– 2; 0); k 2 = 11、B(2; 12)。

20. b の値の場合、関数 y = bx 3 – 2x 2 – 4 のグラフに横軸 x 0 = 2 の点で引かれた接線は点 M(1; 8) を通過しますか?

答え: b = – 3。

21. Ox 軸を頂点とする放物線は、点 A(1; 2) と B(2; 4) を通る直線と点 B で接します。放物線の方程式を求めます。

答え：

22.係数 k のどの値で、放物線 y = x 2 + kx + 1 は Ox 軸に接触しますか?

答え: k = d 2.

23. 直線 y = x + 2 と曲線 y = 2x 2 + 4x – 3 の間の角度を求めます。

29. 関数のグラフの接線と、Ox 軸の正の方向を 45° の角度で持つジェネレーターとの間の距離を求めます。

答え：

30. 直線 y = 4x – 1 に接する y = x 2 + ax + b の形のすべての放物線の頂点の軌跡を求めます。

答え: 直線 y = 4x + 3。

文学

1. ズヴァビッチ L.I.、シュリャポチニク ​​L.Ya.、チンキナ M.V. 代数と解析の始まり: 学童および大学入学者向けの問題 3600 問。 – M.、バスタード、1999 年。
2. モルドコビッチ A. 若い教師のためのセミナー 4。 トピック: 派生アプリケーション。 – M.、「数学」、No. 21/94。
3. 精神作用の漸進的同化理論に基づく知識と技能の形成。 /編 P.Ya. ガルペリーナ、NF タリジナ。 – M.、モスクワ州立大学、1968年。

ある点 x 0 が有限導関数 f (x 0) を持つ関数 f が与えられるとします。 このとき、点 (x 0 ; f (x 0)) を通り、角度係数 f ’(x 0) を持つ直線を接線と呼びます。

微分が点 x 0 に存在しない場合はどうなるのでしょうか? 次の 2 つのオプションがあります。

1. グラフにも接線はありません。 古典的な例は、関数 y = |x | です。 点 (0; 0) で。
2. 接線が垂直になります。 これは、たとえば、点 (1; π /2) における関数 y = arcsin x の場合に当てはまります。

接線方程式

垂直でない直線は、y = kx + b という形式の方程式で与えられます。ここで、k は傾きです。 タンジェントも例外ではなく、ある点 x 0 で方程式を構成するには、この点での関数の値と導関数がわかれば十分です。

そこで、線分上の導関数 y = f ’(x) を持つ関数 y = f (x) を与えてみましょう。 次に、任意の点 x 0 ∈ (a; b) で、この関数のグラフに接線を引くことができます。これは次の方程式で求められます。

y = f ’(x 0) (x − x 0) + f (x 0)

ここで、f ’(x 0) は点 x 0 における導関数の値、f (x 0) は関数自体の値です。

タスク。 関数 y = x 3 が与えられるとします。 この関数のグラフの点 x 0 = 2 における接線の方程式を書きます。

正接方程式: y = f ’(x 0) · (x − x 0) + f (x 0)。 点 x 0 = 2 が与えられますが、値 f (x 0) と f ’(x 0) を計算する必要があります。

まず、関数の値を見つけてみましょう。 ここではすべてが簡単です: f (x 0) = f (2) = 2 3 = 8;
ここで導関数を求めてみましょう: f ’(x) = (x 3)’ = 3x 2;
x 0 = 2 を導関数に代入します。 f ’(x 0) = f ’(2) = 3 2 2 = 12;
合計すると、y = 12 · (x − 2) + 8 = 12x − 24 + 8 = 12x − 16 となります。
これがタンジェント方程式です。

タスク。 関数 f (x) = 2sin x + 5 のグラフの点 x 0 = π /2 における接線の方程式を書きます。

今回は、各アクションの詳細については説明しません。主要な手順のみを示します。 我々は持っています：

f (x 0) = f (π /2) = 2sin (π /2) + 5 = 2 + 5 = 7;
f ’(x) = (2sin x + 5)’ = 2cos x;
f ’(x 0) = f ’(π /2) = 2cos (π /2) = 0;

接線方程式:

y = 0 · (x − π /2) + 7 ⇒ y = 7

後者の場合、直線は水平であることが判明しました。 その角度係数 k = 0 です。これには何も問題はありません。単に極値点に遭遇しただけです。

説明書

点 M における曲線の接線の角度係数を決定します。
関数 y = f(x) のグラフを表す曲線は、点 M の近傍 (点 M 自体も含む) で連続しています。

値 f‘(x0) が存在しない場合は、接線が存在しないか、接線が垂直に延びているかのどちらかです。 これを考慮すると、点 x0 における関数の導関数の存在は、点 (x0, f(x0)) における関数のグラフに接する非垂直接線の存在によるものです。 この場合、接線の角度係数は f "(x0) に等しくなります。したがって、導関数の幾何学的意味が明確になります - 計算 スロープ正接。

文字「a」で示される接点の横座標の値を見つけます。 指定された接点と一致する場合、「a」がその x 座標になります。 値を決定する 機能 f(a)を式に代入して求める 機能横軸の値。

方程式の一次導関数を求める 機能 f’(x) に点「a」の値を代入します。

y = f(a) = f (a)(x – a) として定義される一般接線方程式を使用し、それに a、f(a)、f "(a) の求められた値を代入します。その結果、グラフの解が見つかり、接線になります。

指定された接点が接点と一致しない場合は、別の方法で問題を解決します。 この場合、接線方程式に数字の代わりに「a」を代入する必要があります。 その後、文字「x」と「y」の代わりに座標値を代入します。 与えられたポイント。 「a」が未知数である結果の方程式を解きます。 結果の値を接線方程式に代入します。

問題文で方程式が指定されている場合は、文字「a」を使用して接線の方程式を書きます。 機能目的の接線に対する平行線の方程式。 この後、導関数が必要になります 機能、点「a」の座標に移動します。 適切な値を接線方程式に代入し、関数を解きます。