2 番目の注目すべき極限の公式は、lim x → ∞ 1 + 1 x x = e です。 別の書き方は次のようになります: lim x → 0 (1 + x) 1 x = e。
2 番目の注目すべき限界について話すとき、1 ∞ の形式の不確実性を扱わなければなりません。 無限のレベルの統一。
Yandex.RTB R-A-339285-1
2 番目の顕著な極限を計算する機能が役立つ問題を考えてみましょう。
例1
探す 限界値 x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 。
解決
必要な式を代入して計算してみましょう。
lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 - 2 ∞ 2 + 1 ∞ 2 + 1 4 = 1 - 0 ∞ = 1 ∞
私たちの答えは無限乗でした。 解法を決定するには、不確実性テーブルを使用します。 2 番目の顕著な制限を選択し、変数を変更してみましょう。
t = - x 2 + 1 2 ⇔ x 2 + 1 4 = - t 2
x → ∞ の場合、t → - ∞。
交換後に何が得られたかを見てみましょう:
lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = 1 ∞ = lim x → ∞ 1 + 1 t - 1 2 t = lim t → ∞ 1 + 1 t t - 1 2 = e - 1 2
答え： lim x → ∞ 1 - 2 x 2 + 1 x 2 + 1 4 = e - 1 2 。
例 2
極限 lim x → ∞ x - 1 x + 1 x を計算します。
解決
無限大を代入して次を取得しましょう。
lim x → ∞ x - 1 x + 1 x = lim x → ∞ 1 - 1 x 1 + 1 x x = 1 - 0 1 + 0 ∞ = 1 ∞
答えでは、前の問題と同じ結果が得られたため、再び 2 番目の顕著な制限を使用できます。 次にベースで選択する必要があります べき乗関数全体部分:
x - 1 x + 1 = x + 1 - 2 x + 1 = x + 1 x + 1 - 2 x + 1 = 1 - 2 x + 1
この後、制限は次の形式になります。
lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x
変数を置き換えます。 t = - x + 1 2 ⇒ 2 t = - x - 1 ⇒ x = - 2 t - 1 と仮定しましょう。 x → ∞ の場合、t → ∞。
その後、元の制限内で得られたものを書き留めます。
lim x → ∞ x - 1 x + 1 x = 1 ∞ = lim x → ∞ 1 - 2 x + 1 x = lim x → ∞ 1 + 1 t - 2 t - 1 = = lim x → ∞ 1 + 1 t - 2 t 1 + 1 t - 1 = lim x → ∞ 1 + 1 t - 2 t lim x → ∞ 1 + 1 t - 1 = = lim x → ∞ 1 + 1 t t - 2 1 + 1 ∞ = e - 2 · (1 + 0) - 1 = e - 2
この変換を実行するために、限界と累乗の基本特性を使用しました。
答え： lim x → ∞ x - 1 x + 1 x = e - 2 。
例 3
極限 lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 を計算します。
解決
lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + 1 x 3 1 + 2 x - 1 x 3 3 2 x - 5 x 4 = = 1 + 0 1 + 0 - 0 3 0 - 0 = 1 ∞
その後、2 番目の大きな制限を適用するように関数を変換する必要があります。 以下の結果が得られました。
lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = 1 ∞ = lim x → ∞ x 3 - 2 x 2 - 1 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5
lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 × 2 - 1 × 3 + 2 × 2 - 1 - 2 × 2 + 2 - 2 × 2 + 2 × 3 + 2 × 2 - 1 3 × 4 2 × 3 - 5
なぜなら今私たちは 同じ指標分数の分子と分母に度がかかると (6 に等しい)、無限大における分数の極限は次のようになります。 比率に等しいより高いべき乗で与えられた係数。
lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 2 x 2 + 2 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 6 2 = lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3
t = x 2 + 2 x 2 - 1 - 2 x 2 + 2 を代入すると、2 番目の注目すべき制限が得られます。 意味:
lim x → ∞ 1 + - 2 x 2 + 2 x 3 + 2 x 2 - 1 x 3 + 2 x 2 - 1 - 2 x 2 + 2 - 3 = lim x → ∞ 1 + 1 t t - 3 = e - 3
答え： lim x → ∞ x 3 + 1 x 3 + 2 x 2 - 1 3 x 4 2 x 3 - 5 = e - 3 。
結論
不確実性 1 ∞、つまり 無限べき乗に対する単一性はべき乗則の不確実性であるため、指数関数の極限を見つけるためのルールを使用して明らかにできます。
テキスト内のエラーに気付いた場合は、それを強調表示して Ctrl+Enter を押してください。
いくつかの顕著な限界がありますが、最も有名なのは 1 番目と 2 番目の顕著な限界です。 これらの制限の注目すべき点は、これらの制限が広く使用されており、その助けを借りて、多くの問題で遭遇する他の制限を見つけることができることです。 これが、このレッスンの実践部分で行うことです。 問題を 1 つ目または 2 つ目の顕著な限界値まで削減して問題を解決する場合、これらの限界値は偉大な数学者によって長い間推定されてきたため、問題に含まれる不確実性を明らかにする必要はありません。
最初の顕著な限界は、同じ円弧に対する無限小円弧の正弦の比率の限界と呼ばれ、ラジアン単位で表されます。
最初の顕著な限界における問題の解決に進みましょう。 注: 限界記号の下に三角関数がある場合、これはほぼ 確かな兆候この式は最初の顕著な限界に達する可能性があるということです。
例1.限界を見つけてください。
解決。 代わりに置換 バツゼロは不確実性をもたらします。
.
分母は正弦なので、式は最初の顕著な限界に達することができます。 変換を開始しましょう。
.
分母は 3 つの X の正弦ですが、分子には X が 1 つしかありません。つまり、分子に 3 つの X を取得する必要があることを意味します。 何のために？ 3を紹介します バツ = あるそして式を取得します。
そして、最初の注目すべき限界のバリエーションに到達します。
なぜなら、この式のどの文字 (変数) が X の代わりになるかは重要ではないからです。
X を 3 で乗算し、すぐに除算します。
.
最初に注目すべき限界に従って、分数式を次のように置き換えます。
これで、最終的にこの制限を解決できるようになります。
.
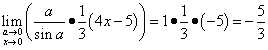例2。限界を見つけてください。
解決。 直接置換すると、再び「ゼロ除算」の不確実性が生じます。
.
最初の顕著な制限を得るには、分子の正弦記号の下の x と分母の x だけが同じ係数を持つ必要があります。 この係数を 2 とします。これを行うには、以下のように x の現在の係数を想像し、分数で演算を実行すると、次のようになります。
.
例 3.限界を見つけてください。
解決。 代入すると、再び「ゼロをゼロで割った」不確実性が生じます。
.
おそらく、元の式から、最初の素晴らしい制限と最初の素晴らしい制限を乗算して取得できることはすでに理解されていると思います。 これを行うには、分子の x と分母の正弦の 2 乗を同じ係数に分解し、x と正弦に同じ係数を取得するために、分子の x を 3 で割ってすぐに乗算します。 3 により、次の結果が得られます。
.
例4.限界を見つけてください。
解決。 もう一度、不確実性「ゼロ除算ゼロ」が得られます。
.
最初の 2 つの顕著な限界の比を得ることができます。 分子と分母の両方を x で割ります。 次に、sine と xes の係数が一致するように、上の x に 2 を掛けてすぐに 2 で割り、下の x に 3 を掛けてすぐに 3 で割ります。次のようになります。
例5.限界を見つけてください。
解決。 そして再び「ゼロ除算ゼロ」の不確実性:
三角法から、タンジェントはサインとコサインの比であり、コサインはゼロであることを思い出します。 1に等しい。 変換を実行すると、以下が得られます。
.
例6。限界を見つけてください。
解決。 限界の符号の下にある三角関数は、最初の顕著な限界の使用を再度示唆します。 サインとコサインの比として表します。
素晴らしい限界を見つけるこれは、極限理論を学ぶ多くの 1 年生と 2 年生だけでなく、一部の教師にとっても困難です。
最初の顕著な極限の公式
最初の注目すべき限界の結果
数式で書いてみましょう
1. 2. 3. 4. しかし、顕著な限界値の一般的な公式自体は、試験やテストにおいては何の役にも立ちません。 重要なのは、実際のタスクは、上記の式に到達する必要があるように構築されているということです。 そして、授業を欠席したり、欠席中にこのコースを学習したり、自分が説明している内容を必ずしも理解していない教師に指導を受けたりする学生の大多数は、最も初歩的な例を顕著な限界まで計算することができません。 最初の顕著な極限の公式から、それらの助けを借りて、三角関数を使用した式のゼロで割ったタイプ 0 の不確実性を研究できることがわかります。 まず最初の顕著な限界のいくつかの例を検討し、次に 2 番目の顕著な限界を検討してみましょう。
例 1. 関数 sin(7*x)/(5*x) の極限を求める
解決策: ご覧のとおり、制限の下にある関数は最初の顕著な制限に近いですが、関数自体の制限は明らかに 1 に等しくありません。 この種の限界に関するタスクでは、正弦の下の変数に含まれるのと同じ係数を持つ変数を分母で選択する必要があります。 この場合は、割って7を掛けます。 
一部の人にとっては、そのような詳細は不必要に思えるかもしれませんが、制限が難しいほとんどの学生にとっては、ルールをよりよく理解し、理論的な内容を習得するのに役立ちます。
また、ある場合は、 逆方向から見た図関数も最初の顕著な制限です。 そしてすべては素晴らしい限界が 1 に等しいからです
同じルールが最初の顕著な制限の結果にも適用されます。 したがって、「最初の注目すべき限界は何ですか?」と問われたら、 迷わず単位ですと答えるべきです。
例 2. 関数 sin(6x)/tan(11x) の極限を求める
解決策: 最終結果を理解するために、次の形式で関数を記述してみましょう。 
顕著な制限のルールを適用するには、係数を乗算および除算します。
次に、関数の積から限界の積までの極限を書きます。 
それなし 複雑な数式チャスカの限界を見つけた 三角関数。 簡単な公式をマスターするには、2 と 4 の極限を考え出して見つけてみてください。これは、1 つの素晴らしい極限の結果として得られる公式です。 さらに複雑な問題を見ていきます。
例 3: 極限 (1-cos(x))/x^2 を計算します。
解決策: 代入によってチェックすると、不確実性は 0/0 になります。 多くの人は、このような例を 1 つの顕著な制限に縮小する方法を知りません。 ここでは三角関数の公式を使用する必要があります 
この場合、制限は明確な形に変わります 
私たちは機能を驚くべき限界の 2 乗まで削減することに成功しました。
例 4: 限界を見つける
解決策: 置換すると、おなじみの機能 0/0 が得られます。 ただし、変数はゼロではなく円周率になる傾向があります。 したがって、最初の顕著な制限を適用するには、新しい変数がゼロになるように変数 x にそのような変更を実行します。 これを行うには、分母を新しい変数 Pi-x=y として表します。 
したがって、前のタスクで与えられた三角関数の公式を使用すると、例は 1 つの注目すべき限界に減らされます。
例 5: 制限値の計算 
解決策: 最初は、制限を単純化する方法が明確ではありません。 しかし、例があるので、答えがあるはずです。 変数が 1 になるという事実は、代入時にゼロと無限を乗算した形式の特徴を与えるため、接線は次の式を使用して置換する必要があります。 
この後、必要な不確実性 0/0 が得られます。 次に、極限内の変数の変更を実行し、コタンジェントの周期性を使用します。 
最後の置換により、顕著な制限の系 1 を使用できるようになります。
2 番目の注目すべき限界は指数関数に等しい
これは古典的な問題ですが、実際の極限問題では必ずしも到達するのが簡単ではありません。
計算で必要になるのは 限界は 2 番目の顕著な限界の結果です。
1. 
2. 
3. 
4.
2 番目の顕著な限界とその結果のおかげで、ゼロをゼロで割る、1 の無限乗、無限を無限で割るなどの不確実性を調査することができ、さらには同次数まで調べることができます。 
知り合いになり始めましょう 簡単な例.
例6。 関数の極限を求める
解決策: 2 番目の顕著な制限を直接適用しても機能しません。 まず、括弧内の項の逆数のように見えるように指数を変換する必要があります。 
これは、2 番目の顕著な極限まで還元し、本質的には、極限の結果の 2 番目の公式を演繹するテクニックです。
例7。 関数の極限を求める
解決策: 素晴らしい極限の帰結 2 の式 3 に対するタスクがあります。 ゼロを代入すると、0/0 の形式の特異点が得られます。 ルールの制限を上げるには、変数が対数と同じ係数を持つように分母を回転させます。 
理解しやすく、試験でも実行しやすいです。 学生が限界値を計算するのは次の問題から始まります。
例8. 関数の極限を計算する[(x+7)/(x-3)]^(x-2) 
解決策: タイプ 1 の無限乗特異点があります。 私の言うことが信じられない場合は、どこでも「X」を無限大に置き換えて確認してください。 ルールを構築するには、分子を括弧内の分母で割ります。これを行うには、まず操作を実行します。 
極限に式を置き換えて素敵な2つの極限に変えてみましょう 
制限は 10 の指数乗に等しくなります。 変数を伴う項である定数は、括弧内と次数の両方で、「天気」を導入しません。これは覚えておく必要があります。 そして、先生が「インジケーターを変換したらどうですか?」と尋ねたら、 (この例では x-3)、次に、「変数が無限大になる傾向がある場合、それに 100 を加算するか、1000 を減算しても、制限は以前と同じままになります。」と言います。
このタイプの制限を計算する 2 番目の方法があります。 それについては次のタスクで説明します。
例9。 限界を見つける 
解決策: 次に、分子と分母の変数を取り出して、ある特徴を別の特徴に変えてみましょう。 最終値を取得するには、注目すべき限界の系 2 の公式を使用します。 
例10。 関数の極限を求める
解決策: 誰もが指定された制限を見つけられるわけではありません。 制限を 2 に上げるには、sin (3x) が変数であり、指数を回す必要があると想像してください。 
次に、インジケーターをべき乗として書きます。 
中間引数は括弧内に記載されています。 1 番目と 2 番目の顕著な制限を使用した結果、指数関数の 3 乗が得られました。
例11. 関数の極限を計算する sin(2*x)/ln(3*x+1)
解決策: 0/0 という形式の不確実性があります。 さらに、両方の素晴らしい制限を使用するように関数を変換する必要があることがわかります。 先ほどの数学的変換を実行してみましょう 
さらに、問題なく、制限は値を取得します 
関数を素早く書き出して、1 つ目または 2 つ目の素晴らしい制限まで減らすことを学べば、課題、テスト、モジュールでどれだけ自由に感じることができるかということです。 限界値を求めるための指定された方法を覚えるのが難しい場合は、いつでも限界値に関するテスト用紙を当社に注文できます。
これを行うには、フォームに記入し、データを提供し、例を含むファイルを添付します。 私たちは多くの学生をサポートしてきました。あなたもお手伝いできます。
このオンライン数学計算機は、必要な場合に役立ちます 関数の極限を計算する。 プログラム ソリューションの限界問題に答えを与えるだけでなく、 説明付きの詳細な解決策、つまり 限度額の計算プロセスを表示します。
このプログラムは高校生にも役立つかもしれません 中学校に備えて テスト統一州試験の前に知識をテストする試験では、保護者が数学や代数学の多くの問題の解決策を管理することができます。 それとも、家庭教師を雇ったり、新しい教科書を購入したりするには高すぎるのでしょうか? それとも、できるだけ早く終わらせたいだけですか？ 宿題数学か代数学でしょうか？ この場合、詳細な解決策を備えた当社のプログラムを使用することもできます。
このようにして、問題解決の分野での教育レベルが向上しながら、自分自身のトレーニングや弟や妹のトレーニングを行うことができます。
関数式を入力してください制限値の計算
この問題を解決するために必要な一部のスクリプトが読み込まれていないため、プログラムが動作しない可能性があることが判明しました。
AdBlock が有効になっている可能性があります。
この場合は、無効にしてページを更新してください。
解決策を表示するには、JavaScript を有効にする必要があります。
ここでは、ブラウザで JavaScript を有効にする方法について説明します。
なぜなら 問題を解決したい人はたくさんいます。あなたのリクエストはキューに入れられています。
数秒以内に解決策が下に表示されます。
お待ちください 秒...
もし、あんたが ソリューションのエラーに気づきました、これについてフィードバック フォームに記入できます。
忘れてはいけない どのタスクを指定するかあなたが何を決めるか フィールドに入力します.
私たちのゲーム、パズル、エミュレーター:
ちょっとした理論。
x->x 0 における関数の極限
関数 f(x) を集合 X 上で定義し、点を \(x_0 \in X\) または \(x_0 \notin X\) とします。
X から、x 0 とは異なる一連の点を取得してみましょう。
x 1 、 x 2 、 x 3 、 ...、 x n 、 ... (1)
x* に収束します。 このシーケンスの各点の関数値も数値シーケンスを形成します
f(x 1)、f(x 2)、f(x 3)、...、f(x n)、... (2)
そしてその限界が存在するという疑問を提起することができます。
意味。 数値 A は、引数 x の値のシーケンス (1) が x 0 と異なる場合、点 x = x 0 (または x -> x 0) における関数 f(x) の極限と呼ばれます。 x 0 に収束すると、対応する値関数のシーケンス (2) は数値 A に収束します。
$$ \lim_(x\to x_0)( f(x)) = A $$
関数 f(x) は点 x 0 で極限を 1 つだけ持つことができます。 これは、次のシーケンスが成り立つという事実から導かれます。
(f(x n)) の制限は 1 つだけです。
関数の限界には別の定義があります。
意味数値 A は、任意の数値 \(\varepsilon > 0\) に対して、すべての \ に対して次のような数値 \(\delta > 0\) が存在する場合、点 x = x 0 における関数 f(x) の極限と呼ばれます。 (x \in X, \; x \neq x_0 \)、不等式 \(|x-x_0| を満たす) 論理記号を使用すると、この定義は次のように書くことができます。
\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| 不等式 \(x \neq x_0 , \; |x-x_0| 最初の定義は限界の概念に基づいています。 数列、そのため、これは「シーケンス言語」定義と呼ばれることがよくあります。 2 番目の定義は、「言語 \(\varepsilon - \delta \) による」定義と呼ばれます。
関数の極限に関するこれら 2 つの定義は同等であり、特定の問題を解決するのにどちらがより便利であるかに応じて、どちらかを使用できます。
「数列の言語における」関数の極限の定義は、ハイネによる関数の極限の定義とも呼ばれ、「言語 \(\varepsilon - における) 関数の極限の定義」とも呼ばれることに注意してください。 \delta \)」は、コーシーによれば関数の極限の定義とも呼ばれます。
x->x 0 - および x->x 0 + における関数の極限
以下では、次のように定義される関数の片側極限の概念を使用します。
意味数 A は、任意の数列 (1) が x 0 に収束し、その要素 x n が x 0 より大きい (小さい) 場合、点 x 0 における関数 f(x) の右 (左) 極限と呼ばれます。対応する数列 (2) は A に収束します。
象徴的には次のように書かれます。
$$ \lim_(x \to x_0+) f(x) = A \; \left(\lim_(x \to x_0-) f(x) = A \right) $$
関数の片側極限を「言語 \(\varepsilon - \delta \)」で同等に定義することができます。
意味数値 A は、任意の \(\varepsilon > 0\) に対して \(\delta > 0\) が存在し、すべての x が次を満たす場合、点 x 0 における関数 f(x) の右 (左) 極限と呼ばれます。不等式 \(x_0 記号エントリ:
証拠：
まず、次の数列の場合の定理を証明しましょう。 
ニュートンの二項公式によれば、次のようになります。
得たと仮定すると
この等式 (1) から、n が増加するにつれて、右辺の正の項の数が増加することがわかります。 また、n が増加すると数値は減少しますので、値は 
増加しています。 したがって、シーケンスは 
(2)*それが有界であることを示します。 等式の右側の各括弧を 1 に置き換えると、右側が増加し、不等式が得られます。
結果の不等式を強化して、分数の分母にある 3、4、5、... を数値 2 に置き換えてみましょう。項の合計の公式を使用して括弧内の合計を求めます。 等比数列： それが理由です 
(3)*
したがって、シーケンスは上から制限され、不等式 (2) と (3) が満たされます。 
したがって、ワイエルシュトラスの定理 (数列の収束基準) に基づいて、数列は 
単調増加し、制限されます。つまり、文字 e で示される限界があることを意味します。 それらの。 
2 番目の注目すべき極限が x の自然値に当てはまることがわかっているので、実数 x に対する 2 番目の注目すべき極限を証明します。つまり、次のことを証明します。 
。 2 つのケースを考えてみましょう。
1. x の各値を 2 つの正の整数で囲みます。ここで、 は x の整数部分です。 => =>
の場合、したがって、制限に従って 
我々は持っています
極限の有無の基準（中間関数の極限について）に基づく 
2. しましょう。 置換 − x = t を行ってみましょう。
これら 2 つのケースから、次のことがわかります。 
本当のxの場合。
結果：
9 .) 無限小の比較。 極限において無限小を等価なものに置き換えることに関する定理と無限小の主要部分に関する定理。
関数を a( バツ) と b( バツ） – b.m. で バツ ® バツ 0 .
定義。
1)あ( バツ) 呼ばれた ～よりも高次の無限小 b (バツ) もし
書き留めます: a( バツ) = o(b( バツ)) .
2)あ( バツ) そして b( バツ)呼ばれます 同じ次数の無限小、 もし
ここで CÎℝと C¹ 0 .
書き留めます: a( バツ) = ○(b( バツ)) .
3)a( バツ) そして b( バツ) 呼ばれます 同等 , もし
書き留めます: a( バツ) ~ b( バツ).
4)a( バツ) は k 次の相対的な無限小と呼ばれます
絶対的に無限小 b( バツ),
無限小の場合あ( バツ)そして(b( バツ))k 同じ順序を持つ、つまり もし
ここで CÎℝと C¹ 0 .
定理 6 (無限小を同等のものに置き換えることについて)。
させてあ( バツ), b( バツ), 1 ( バツ), b1( バツ)–b.m. xで ® バツ 0 。 もしあ( バツ) ~ a 1 ( バツ), b( バツ) ~ b1 ( バツ),
それ 
証明: a( バツ) ~ a 1 ( バツ), b( バツ) ~ b1 ( バツ)、 それから
定理７（微小本体について）。
させてあ( バツ)そして b( バツ)–b.m. xで ® バツ 0 、 そして b( バツ)–b.m. よりも高次のあ( バツ).
= , a 以来 b( バツ) – a( よりも高次 バツ)、つまり、 
から それは明らかです( バツ) + b( バツ) ~ a( バツ)
10) ある点における関数の連続性 (イプシロンデルタの用語で言えば、幾何学的限界) 片側連続性。 区間、セグメント上の連続性。 連続関数のプロパティ。
1. 基本的な定義
させて f(バツ) は点の近傍で定義されます バツ 0 .
定義1. 関数 f(バツ) 呼ばれた ある点で連続する バツ 0 等式が真の場合
ノート.
1) 定理 5 §3 により、等式 (1) は次の形式で書くことができます。
条件(2) – 片側限界の言語における、ある点における関数の連続性の定義.
2) 等式 (1) は次のように書くこともできます。
彼らはこう言います：「関数がある点で連続であれば、 バツ 0 の場合、限界と関数の符号を入れ替えることができます。」
定義 2 (電子言語)。
関数 f(バツ) 呼ばれた ある点で連続する バツ 0 もし"e>0 $d>0 そのような, 何
×の場合ОU( バツ 0 , d) (つまり | バツ – バツ 0 | < d),
それからf(バツ)ÎU( f(バツ 0)、e) (つまり | f(バツ) – f(バツ 0) | < e).
させて バツ, バツ 0 Î D(f) (バツ 0 – 固定、 バツ -任意）
D と表します。 バツ= × – × 0 – 引数の増分
D f(バツ 0) = f(バツ) – f(バツ 0) – 点xにおける関数の増分 0
定義 3 (幾何学的)。
関数 f(バツ） の上 呼ばれた ある点で連続する
バツ 0
この時点で、引数の微小な増分が関数の微小な増分に対応する場合、つまり
機能させましょう f(バツ) は間隔 [ バツ 0 ; バツ 0 + d) (間隔 ( バツ 0 – d; バツ 0 ]).
意味。 関数 f(バツ) 呼ばれた ある点で連続する
バツ 0 右に
(左
), 等式が真の場合
それは明らかです f(バツ) 点では連続です バツ 0 Û f(バツ) 点では連続です バツ左右0です。
意味。 関数 f(バツ) 呼ばれた 一定期間連続して e ( ある; b) この間隔のすべての点で連続している場合.
関数 f(バツ) セグメント上では連続と呼ばれます [ある; b] 一定の間隔で連続している場合 (ある; b) 境界点では一方向の連続性があります(つまり、その点で連続 ある右側、ポイントのところ b- 左）。
11) ブレークポイントとその分類
意味。 If 関数 f(バツ) 点 x の近傍で定義される 0 , しかし、この時点では連続していません。 f(バツ) 点 x で不連続と呼ばれる 0 , そしてその点自体 バツ 0 ブレークポイントと呼ばれる 関数 f(バツ) .
ノート.
1) f(バツ) は、点の不完全な近傍で定義できます。 バツ 0 .
次に、対応する関数の一方向連続性を考慮します。
2) β点の定義より バツ 0は関数のブレークポイントです f(バツ) 2 つの場合:
a) U( バツ 0、d)О D(f）、しかし、 f(バツ) 平等は成り立たない
b) U * ( バツ 0、d)О D(f) .
のために 初等関数 b)の場合のみ可能です。
させて バツ 0 – 関数ブレークポイント f(バツ) .
意味。 点x 0 呼ばれた ブレークポイント 私 ある種の if 関数 f(バツ)この時点では左右に有限の制限があります.
これらの制限が等しい場合、点 x 0 呼ばれた 取り外し可能なブレークポイント , さもないと - ジャンプポイント .
意味。 点x 0 呼ばれた ブレークポイント Ⅱ ある種の 関数 f の片側極限の少なくとも 1 つが満たされている場合、(バツ)この時点では等しい¥ あるいは存在しない.
12) 区間上で連続する関数の性質 (ワイエルシュトラスの定理 (証明なし) とコーシーの定理)
ワイエルシュトラスの定理
関数 f(x) が区間上で連続であるとすると、
1)f(x) は次のように制限されます
2) f(x) は区間上の最小値をとり、 最高値
意味: 関数 m=f の値は、任意の x€ D(f) に対して m≤f(x) の場合に最小値と呼ばれます。
関数 m=f の値は、任意の x € D(f) に対して m≥f(x) の場合に最大になると言われます。
この関数は、セグメントのいくつかの点で最小/最大値を取得できます。
f(x 3)=f(x 4)=最大
コーシーの定理。
関数 f(x) がセグメント上で連続で、x が f(a) と f(b) の間に含まれる数であるとすると、f(x 0)= g となる点 x 0 € が少なくとも 1 つ存在します。
